印象に残った入試問題の良問を「今年の1問」と題して取り上げています。志望校への腕試しや，重要項目の確認に是非ご活用下さい。
実際の試験を改訂しているものもあるのでご了承下さい。
四天王寺中
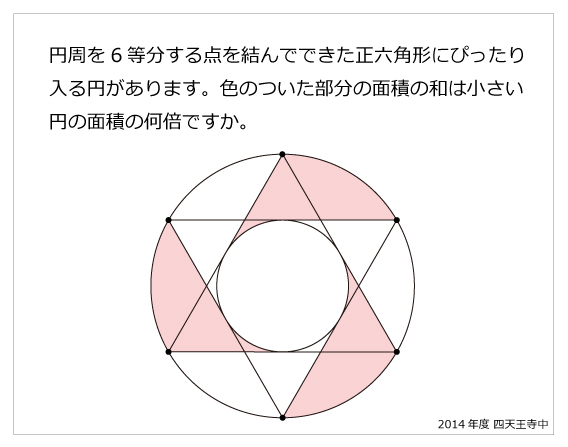
問題文
円周を6等分する点を結んでできた正六角形にぴったり入る円があります。色のついた部分の面積の和は小さい円の面積の何倍ですか。解説
四天王寺中-円と正六角形
算数星人PR
中学受験の通信教育 logix出版
上本町と西宮北口の図形NOTE算数教室
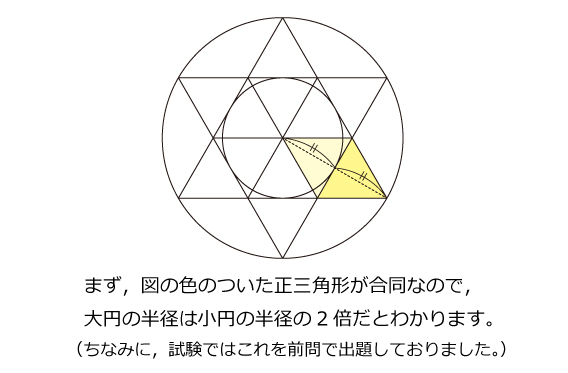
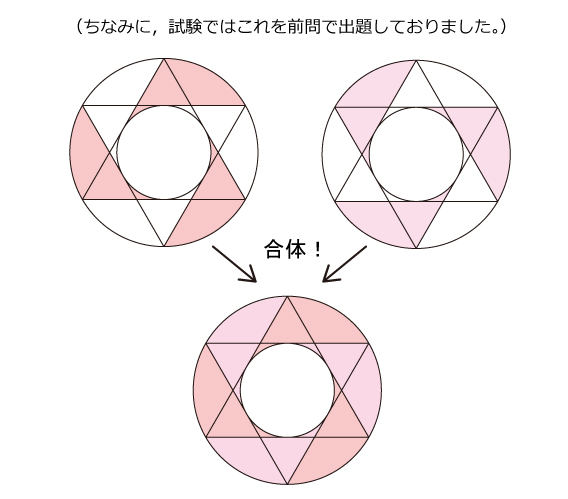
印象に残った入試問題の良問を「今年の1問」と題して取り上げています。志望校への腕試しや，重要項目の確認に是非ご活用下さい。
実際の試験を改訂しているものもあるのでご了承下さい。
中学受験の通信教育 logix出版
上本町と西宮北口の図形NOTE算数教室
「面積の和は小さい円の面積の何倍ですか？」の問題文の問いかけから，
（円の半径を与えたとき）答えは〇〇π(cm^2）になるだろうとわかるので，図形を等積変形するなどをしても，ある程度推測をたてながら解き進めることができるでしょう。
落としてほしくない問題なのですが。。。あまり見かけない問題なので苦戦した生徒も多いであろうと分析しております。