小学生の知の祭典 算数オリンピック!!
受験算数のトレンドを牽引するような新傾向問題の出題が多いことで有名でしょう。その中でも極めて高級な良問,面白い問題をできるだけ取り上げていきたいと思います。
実際の試験を改訂しているものもあるのでご了承下さい。
算数オリンピック

問題文
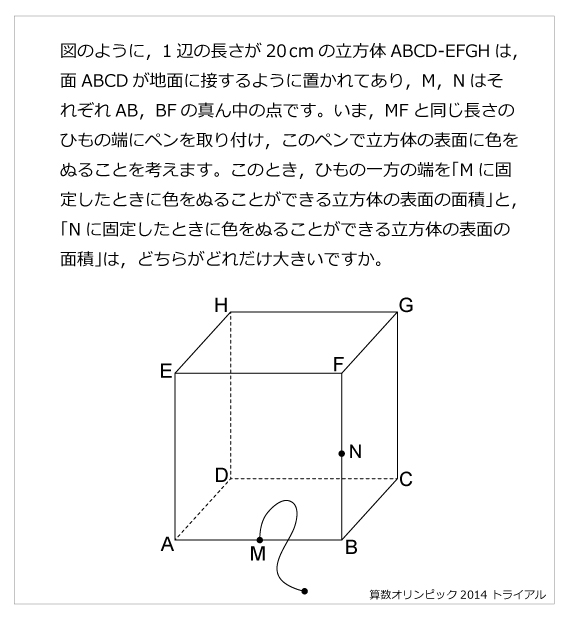
図のように,1辺の長さが20cmの立方体ABCD-EFGHは,面ABCDが地面に接するように置かれてあり,M,NはそれぞれAB,BFの真ん中の点です。いま,MFと同じ長さのひもの端にペンを取り付け,このペンで立方体の表面に色をぬることを考えます。このとき,ひもの一方の端を「Mに固定したときに色をぬることができる立方体の表面の面積」と,「Nに固定したときに色をぬることができる立方体の表面の面積」は,どちらがどれだけ大きいですか。ただし,ペンの太さ,長さは考えず,地面と接している面ABCDには色をぬることもひもやペンが通過できないものとし,必要であれば円周率を3.14として計算しなさい。解説
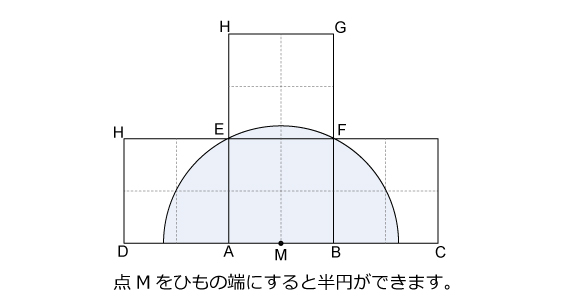
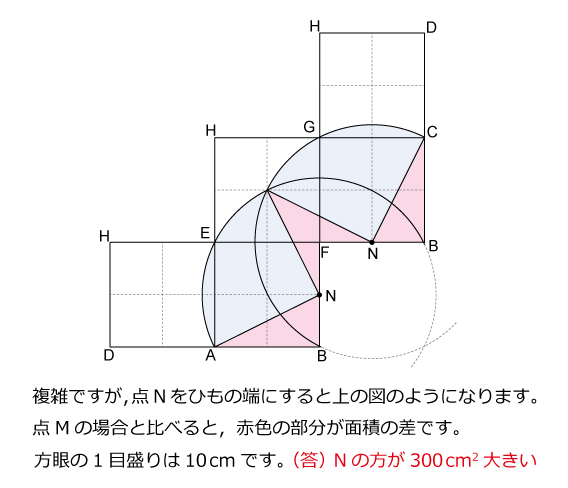
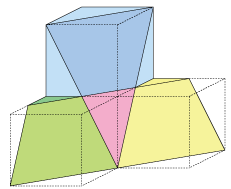
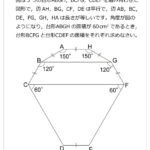
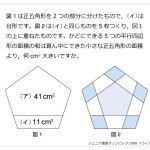

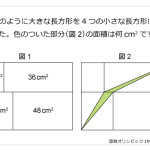
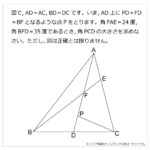
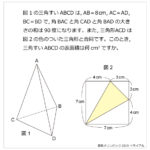

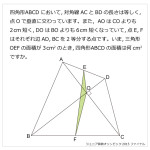








算数オリンピックの立体の問題としては易しいほうの問題だったと思いました。