小学生の知の祭典 算数オリンピック!!
受験算数のトレンドを牽引するような新傾向問題の出題が多いことで有名でしょう。その中でも極めて高級な良問,面白い問題をできるだけ取り上げていきたいと思います。
実際の試験を改訂しているものもあるのでご了承下さい。
算数オリンピック
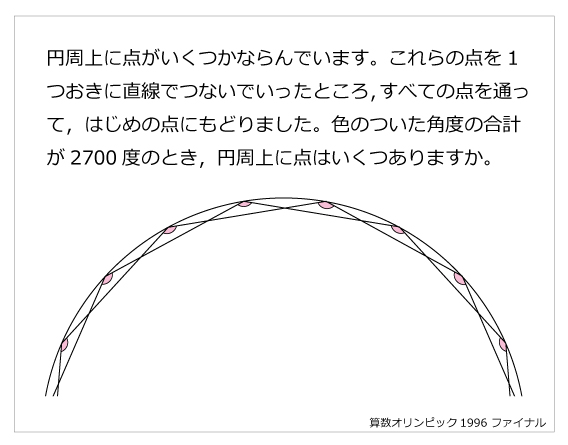
問題文
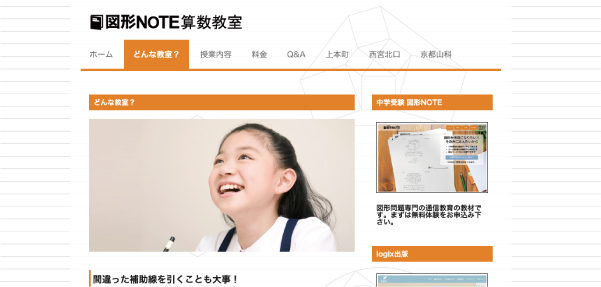
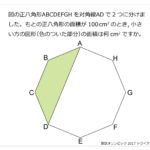
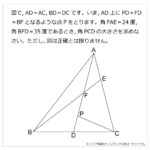
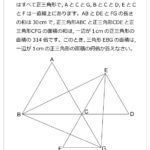
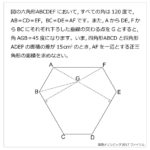
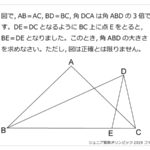
円周上に点がいくつかならんでいます。これらの点を1つおきに直線でつないでいったところ,すべての点を通って,はじめの点にもどりました。色のついた角度の合計が2700度のとき,円周上に点はいくつありますか。解説
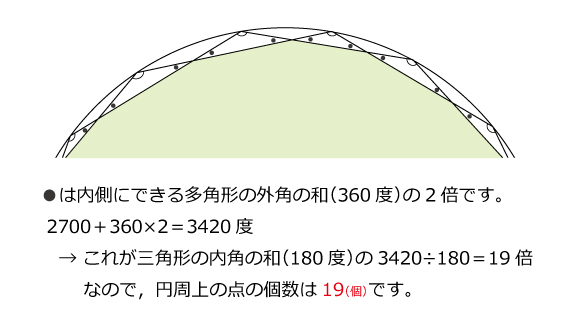


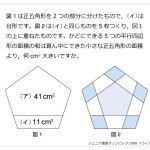








答えは奇数なので,五角形→七角形→九角形→… と規則性を調べても良いと思います。