小学生の知の祭典 算数オリンピック!!
受験算数のトレンドを牽引するような新傾向問題の出題が多いことで有名でしょう。その中でも極めて高級な良問,面白い問題をできるだけ取り上げていきたいと思います。
実際の試験を改訂しているものもあるのでご了承下さい。
算数オリンピック
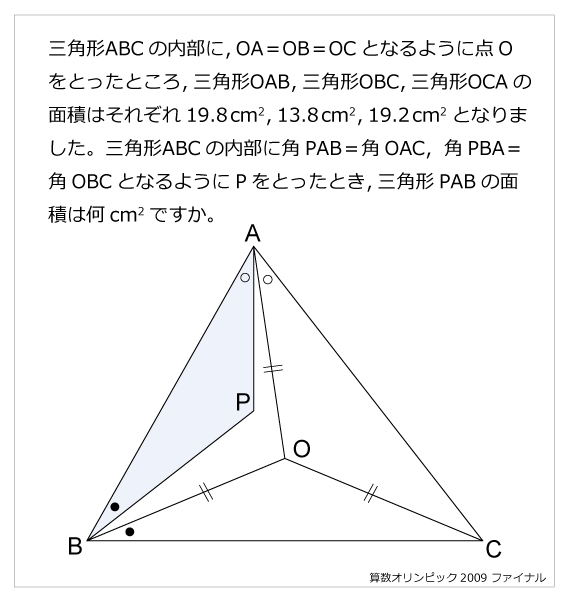
問題文
三角形ABCの内部に,OA=OB=OCとなるように点Oをとったところ,三角形OAB,三角形OBC,三角形OCAの面積はそれぞれ19.8cm2,13.8cm2,19.2cm2となりました。三角形ABCの内部に角PAB=角OAC,角PBA=角OBCとなるようにPをとったとき,三角形PABの面積は何cm2ですか。解説
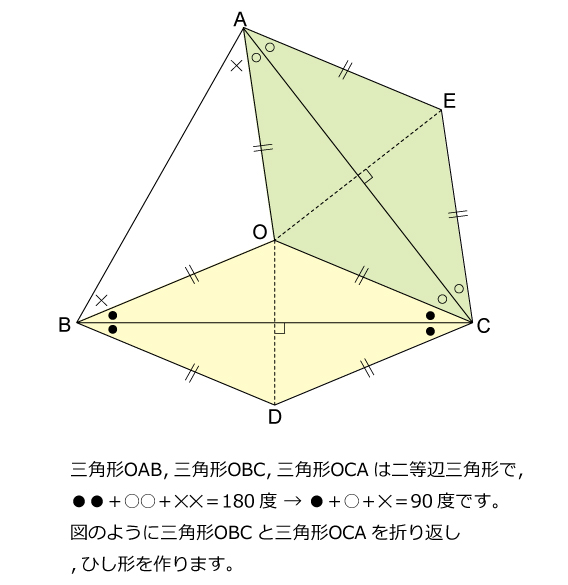
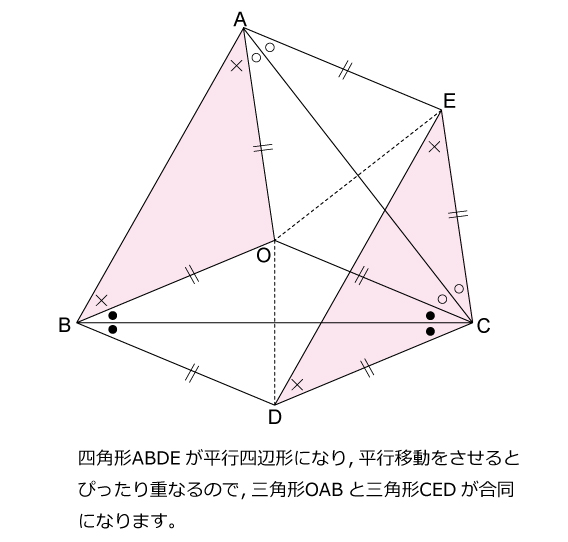
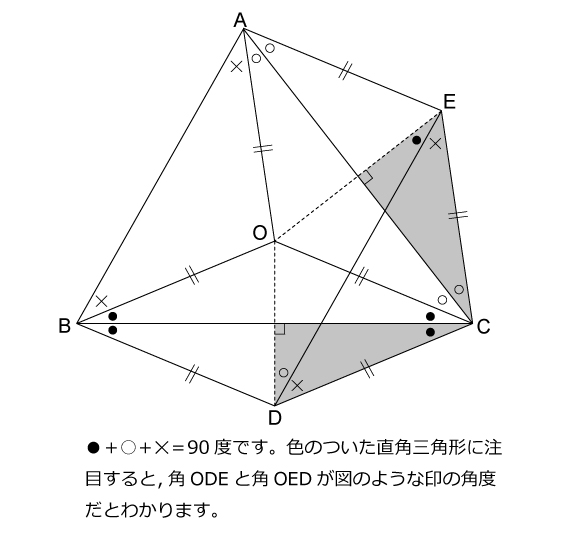
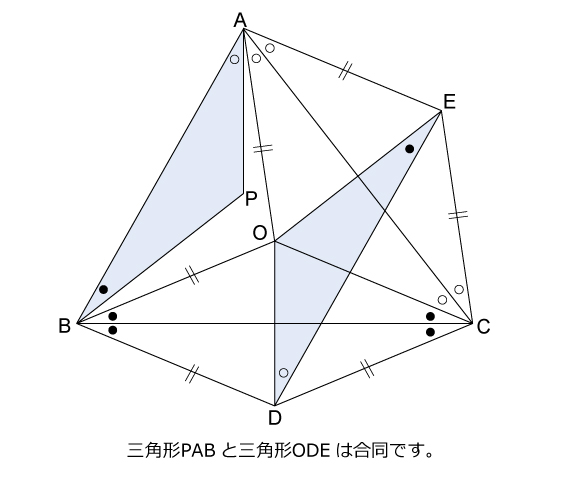
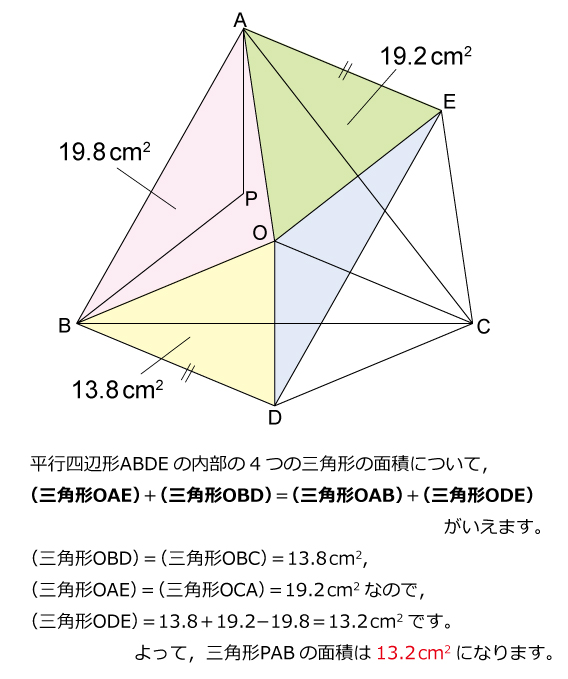

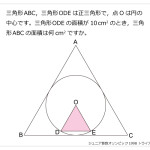
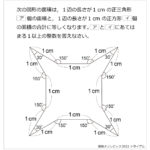
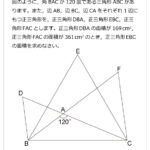
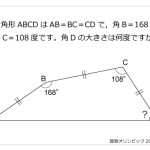
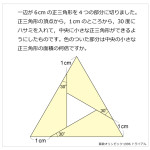
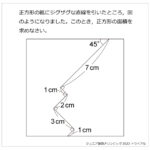
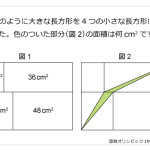








手のつけよう無い難問に対しては,線対称を利用して折り返したり,回転させると解法の糸口が見つかりやすいように個人的に思います。