小学生の知の祭典 算数オリンピック!!
受験算数のトレンドを牽引するような新傾向問題の出題が多いことで有名でしょう。その中でも極めて高級な良問,面白い問題をできるだけ取り上げていきたいと思います。
実際の試験を改訂しているものもあるのでご了承下さい。
算数オリンピック
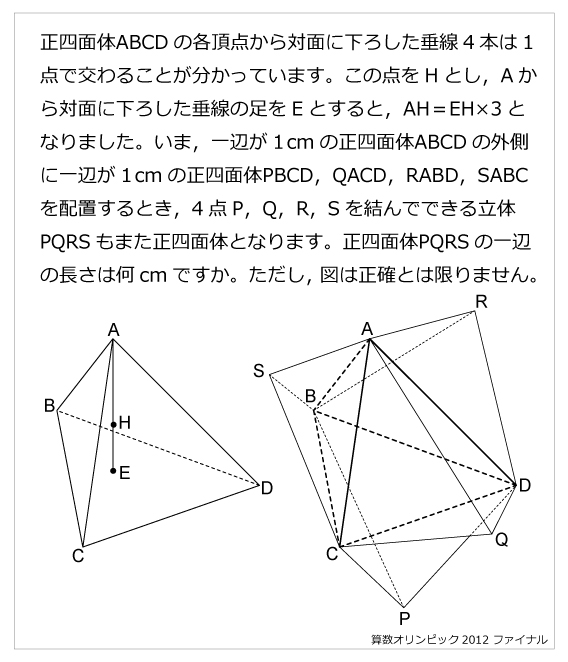
問題文
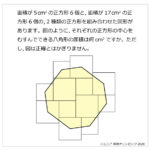
正四面体ABCDの各頂点から対面に下ろした垂線4本は1点で交わることが分かっています。この点をHとし,Aから対面に下ろした垂線の足をEとすると,AH=EH×3となりました。いま,一辺が1cmの正四面体ABCDの外側に一辺が1cmの正四面体PBCD,QACD,RABD,SABCを配置するとき,4点P,Q,R,Sを結んでできる立体PQRSもまた正四面体となります。正四面体PQRSの一辺の長さは何cmですか。ただし,図は正確とは限りません。解説
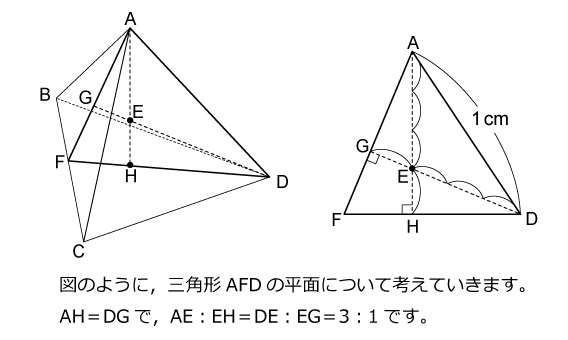
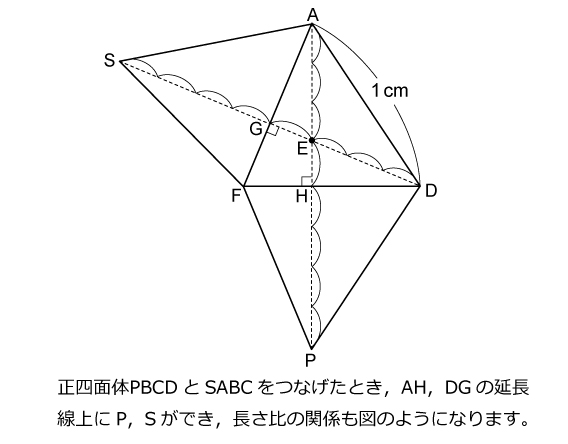
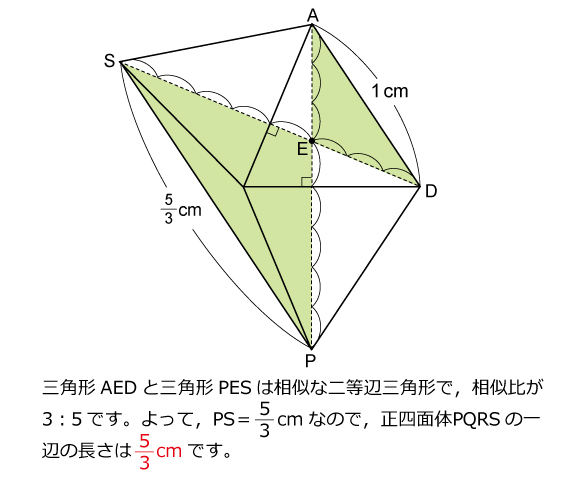
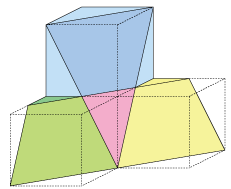

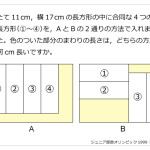
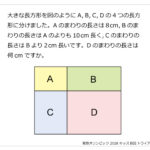








解説をするとスンナリ終了するのですが,実際に何から手をつけて良いのかよく分からなかった問題ではないでしょうか。。。