新連載企画「小学生でもわかる塵劫記」の第5回目です。
 
第1回「俵杉算」
第2回「入れ子算」
第3回「からす算」
第4回「盗人算」
 

 
第5回は「百五減算」です。
 
高学年の向けの記事なので，小3以下の小学生などは大きくなってから是非読んでみましょう！
 

百五減算（あまり問題の応用解法）

 
百五減算（ひゃくごげんざん）
 
105を減らす解法です。105とは，あとで登場しますが，3と5と7の最小公倍数です。
 
では問題。
 

7でわると2あまり，5でわると1あまり，3でわると2あまる最小の数はいくつですか？

 
しっかり勉強をしている6年生であれば一度は拝見したことのある問題でしょう。
 
まずは中学受験生向けの王道解法からさらっと紹介します。
 
解説上，3つの条件をA〜Cとします。
 

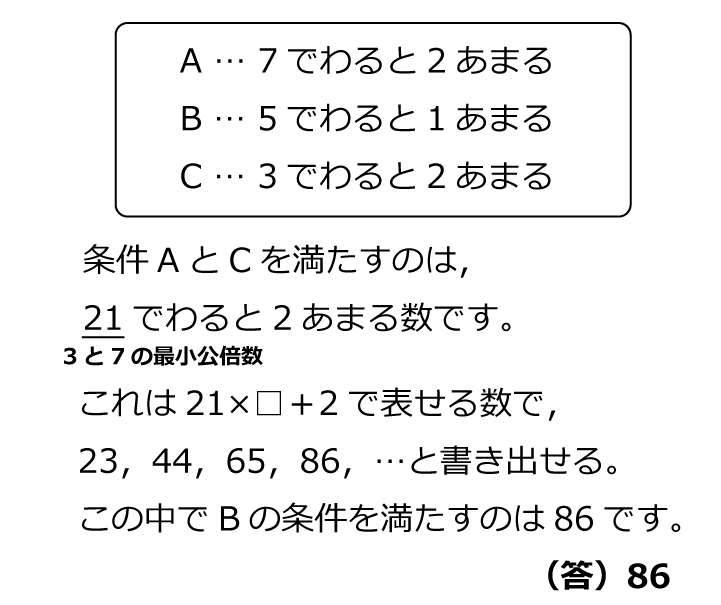
共通の2あまりに注目して2つの条件をコンパクトにするのは定番の方法でしょう。
 
ここではまだ「105を減らす」＝百五減が出てきませんね。
 
塵劫記では少しトリッキーな方法で問題を解いていました。
 
 
-塵劫記での解き方-
 

30と21と140の3つの数が登場しました。
 

最後に105を減らすので，まさに百五減算です。
 
この問題に関して，私自身が中学受験生に塵劫記解法で説明することは到底ないです。
 
この考え方がどこでも役に立つとは思いません。意欲のある受験生は説明を理解できるぐらいで十分だと思います。
 
さて，実はこの問題ですが，あまりが色々異なった場合（一般化）でも数式に数値を当てはめるだけでも解けます。
 

あまりを◯△□とします。もちろん◯は7未満，△は5未満，□は3未満の整数です。
 

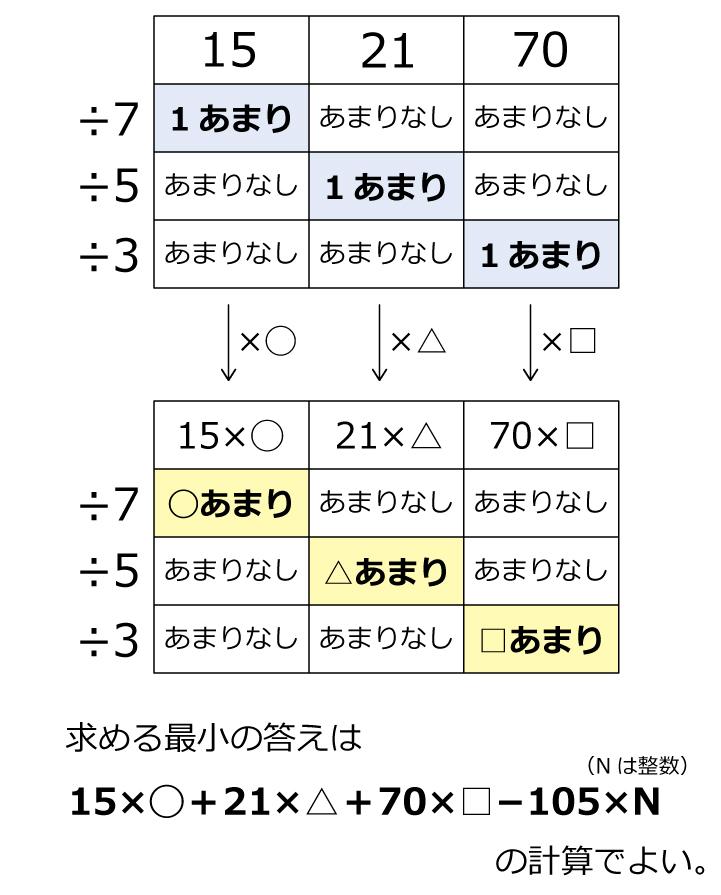
実はこの方法，中国大陸の古い算術書から伝わったもので「孫子の定理」や「中国の剰余定理」といいます。
兵法書の孫子とは関係ありません。
 
このBLOGでは小学生向けに記述しましたが，合同式というもの用いた有名な考え方で証明できます。
 
受験算数だけでは物足りない優秀な受験生は色々調べて見るとよいでしょう。理解出来ないことはないと思います。
 
 
＜P228-229 三目録第十三「百五げんという事」を参照＞
 

 
新編塵劫記三巻の電子画像はこちら
 

（ソース）阪本龍門文庫善本電子画像集
 
 
つづき
【和算】第6回「ねずみ算」」小学生でもわかる塵劫記-じんこうき-