印象に残った入試問題の良問を「今年の1問」と題して取り上げています。志望校への腕試しや,重要項目の確認に是非ご活用下さい。
実際の試験を改訂しているものもあるのでご了承下さい。
東大寺学園中
問題文
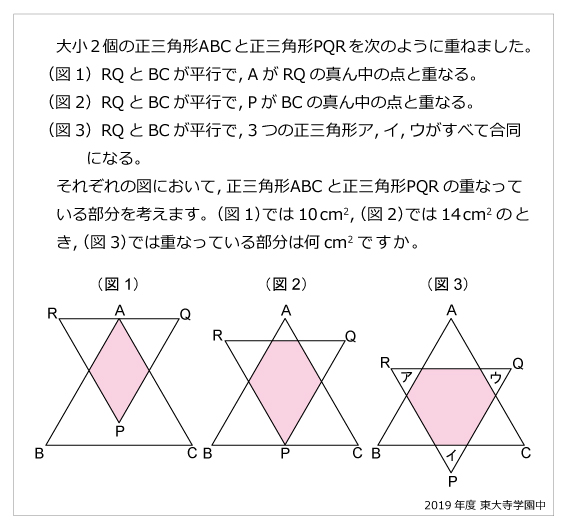
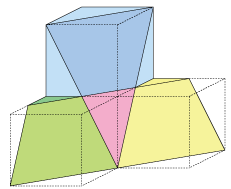
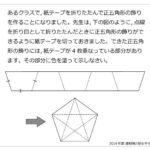
大小2個の正三角形ABCと正三角形PQRを次のように重ねました。(図1)RQとBCが平行で,AがRQの真ん中の点と重なる。
(図2)RQとBCが平行で,PがBCの真ん中の点と重なる。
(図3)RQとBCが平行で,3つの正三角形ア,イ,ウがすべて合同になる。
それぞれの図において,正三角形ABCと正三角形PQRの重なっている部分を考えます。(図1)では10cm2,(図2)では14cm2のとき,(図3)では重なっている部分は何cm2ですか。
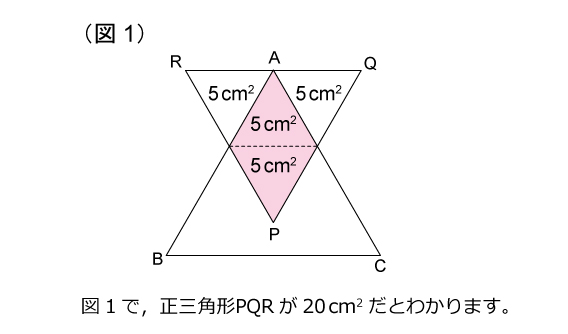
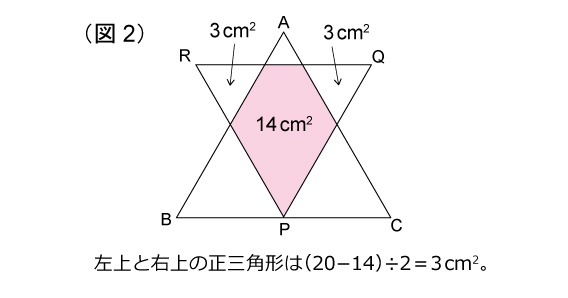
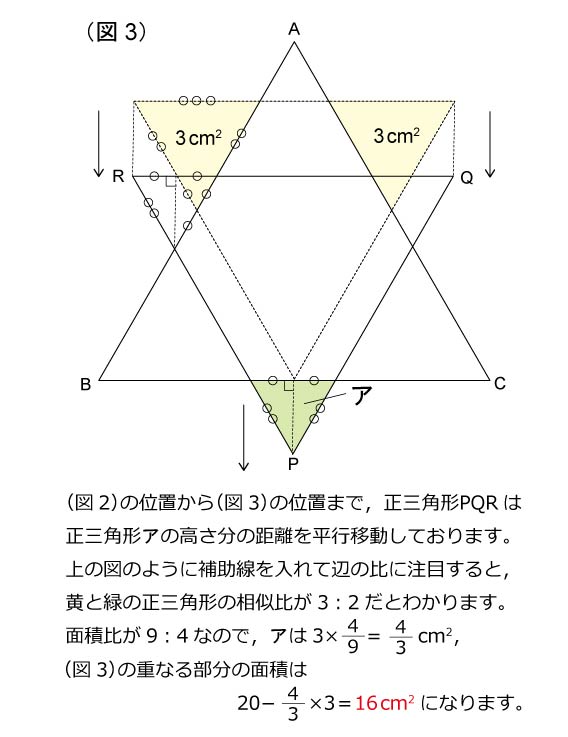
解説
タレコミ
それにしても,ここ3年の東大寺の算数は,【3】(2)のこのポジションに「三角定規」をからめる問題を配置するのが好きのようです。去年は正六角形の周りの円の転がり移動だったかなぁ~。
— 算数大好き (@kimagure_mana) 2019年1月21日

非常に的を射た分析です。勉強になります。











シンプルな設定でしたが,なかなかうまく正解まで運ぶことができなかったのではないでしょうか。
解けそうでなかなか解けない,嫌な問題でしょう。受験生は泥沼にはまらないように!