印象に残った入試問題の良問を「今年の1問」と題して取り上げています。志望校への腕試しや,重要項目の確認に是非ご活用下さい。
実際の試験を改訂しているものもあるのでご了承下さい。
西大和学園中
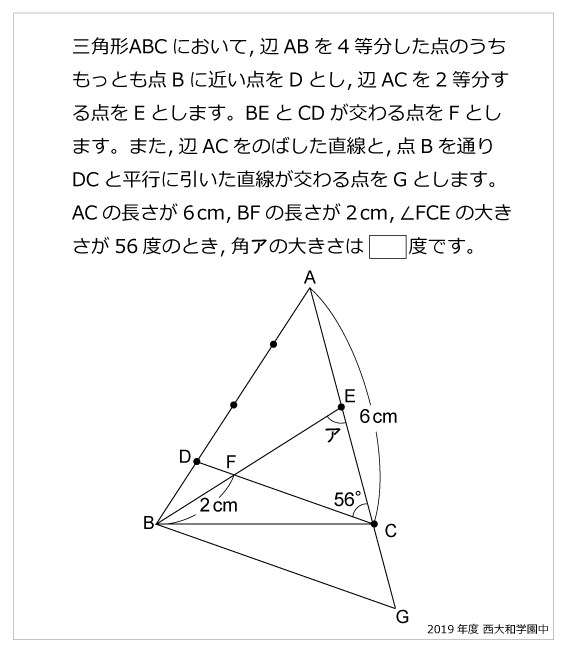
問題文
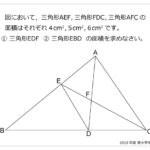
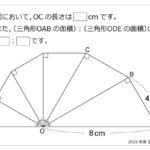
三角形ABCにおいて,辺ABを4等分した点のうちもっとも点Bに近い点をDとし,辺ACを2等分する点をEとします。BEとCDが交わる点をFとします。また,辺ACをのばした直線と,点Bを通りDCと平行に引いた直線が交わる点をGとします。ACの長さが6cm,BFの長さが2cm,∠FCEの大きさが56度のとき,角アの大きさは□度です。解説
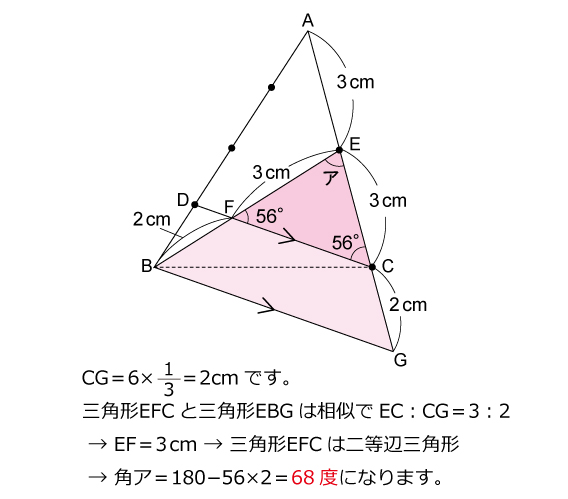
ツイートより
この問題、平行線BGがなくても、ベンツ切りでEF=3cmが簡単に出て二等辺三角形が見えてくるので、問題ができた当初は平行線BGはない設定だったのかな?と勝手に想像しております。
というか、例年の西大和であれば、平行線BGは引かれていないでしょうね…。— なきいるか@別垢(算数隧道研究用) (@naki_iruka_5sz5) 2019年2月3日











しっかり勉強をしてきた受験生であれば,どこかで一度は見かけたことのあるありきたりな問題ばかりとなりました。
その中からまだかろうじて西大和らしさの残った問題だと思い,この問題をピックアップしました。
去年は突然,思考力パズルのような問題も登場し驚かせましたが,今年は,ある意味拍子抜けした塾関係者も多いのではないでしょうか。。。