印象に残った入試問題の良問を「今年の1問」と題して取り上げています。志望校への腕試しや,重要項目の確認に是非ご活用下さい。
実際の試験を改訂しているものもあるのでご了承下さい。
灘中

問題文
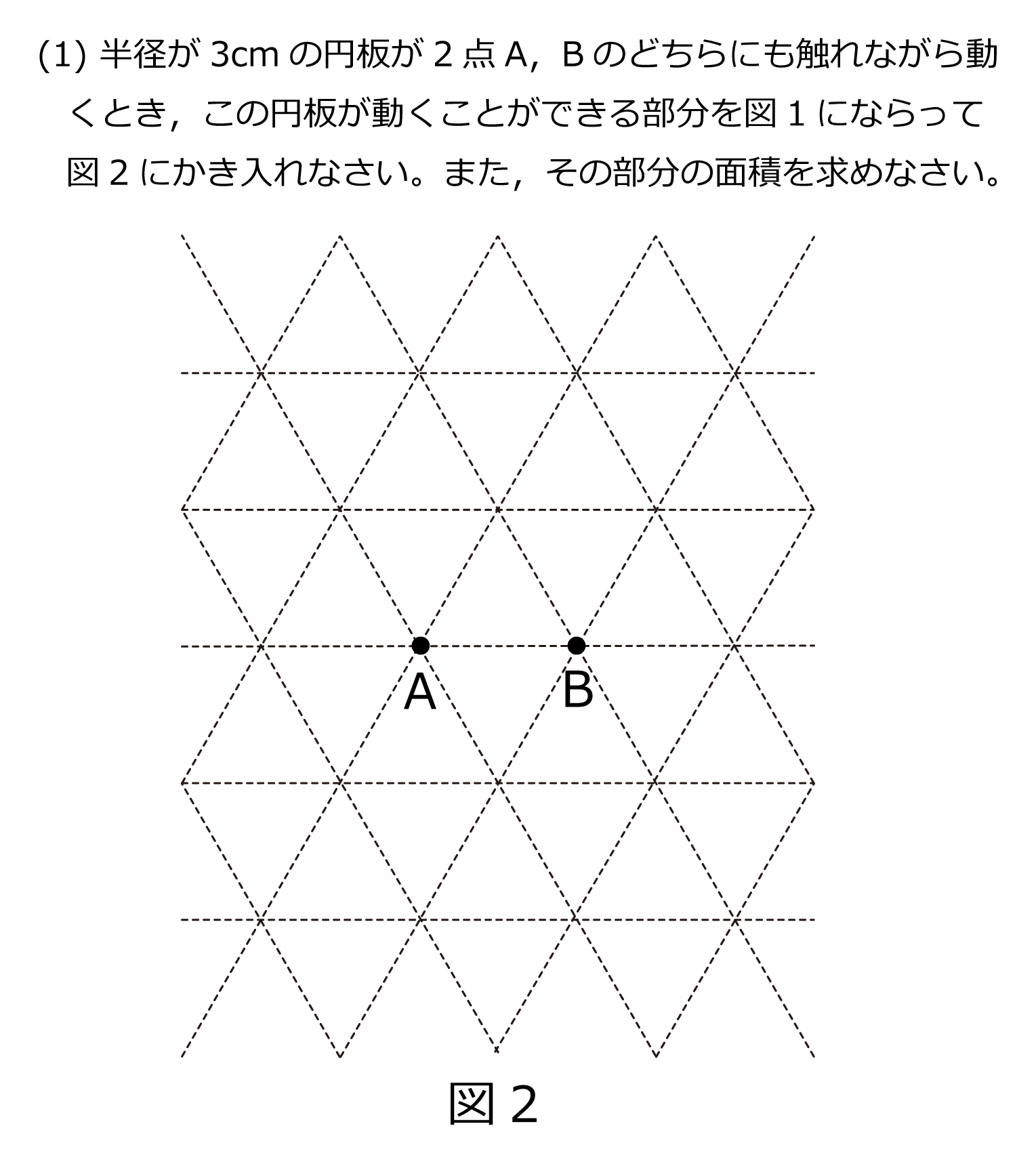
この問題では,1辺の長さが3cmの正三角形の面積を3.9cm2,円周率を3.14として答えなさい。コンパスを使わずに円をかく場合はなるべく丁寧にかきなさい。平面上に3cm離れた2点A,Bと半径が3cmの円板があります。この円板が点Aに触れながら動くとき,円板が動くことができる部分は図1の色のついた部分のようになります。(1) 半径が3cmの円板が2点A,Bのどちらにも触れながら動くとき,この円板が動くことができる部分を図1にならって図2にかき入れなさい。また,その部分の面積を求めなさい。
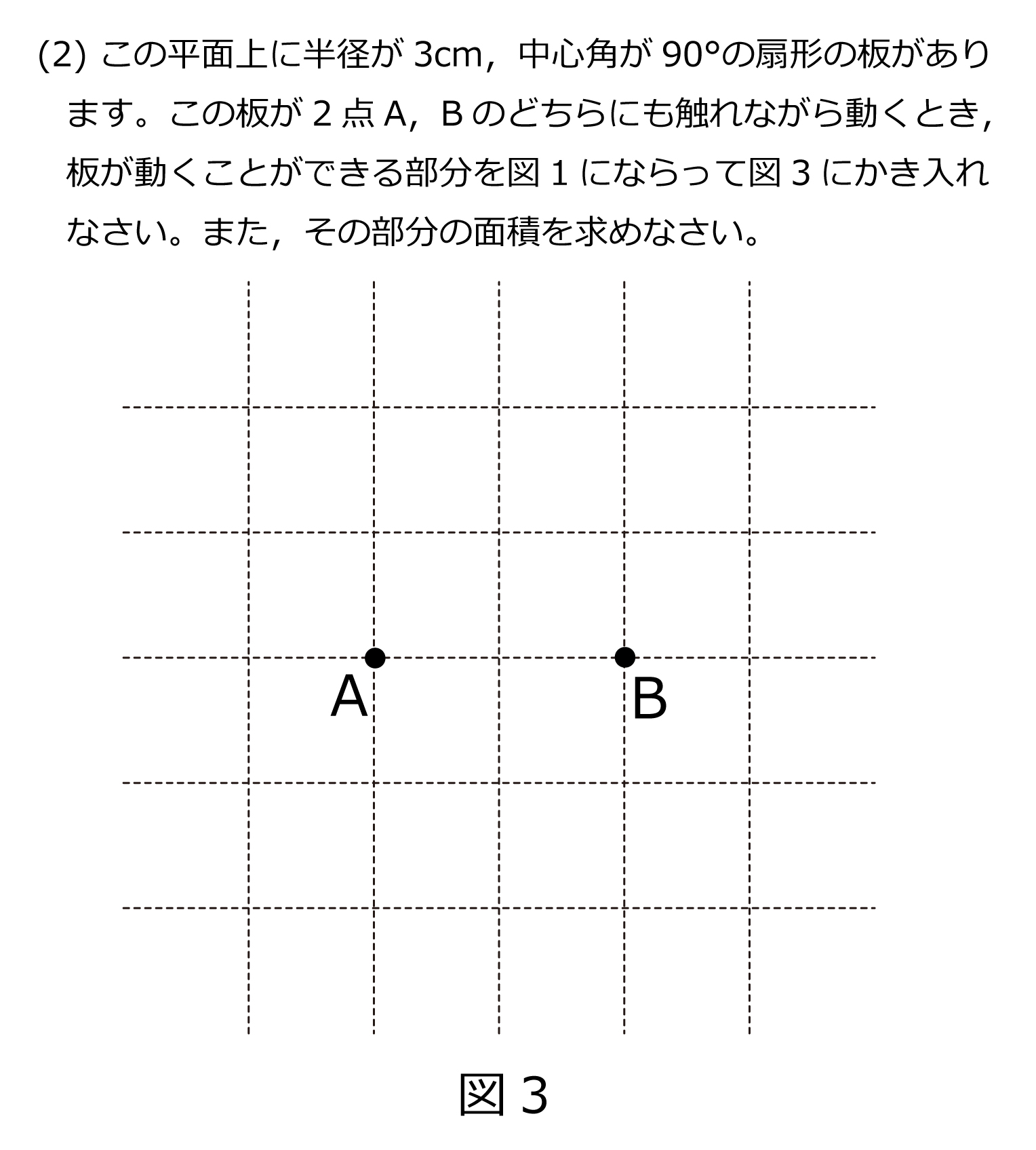
(2) この平面上に半径が3cm,中心角が90°の扇形の板があります。この板が2点A,Bのどちらにも触れながら動くとき,板が動くことができる部分を図1にならって図3にかき入れなさい。また,その部分の面積を求めなさい。
解説
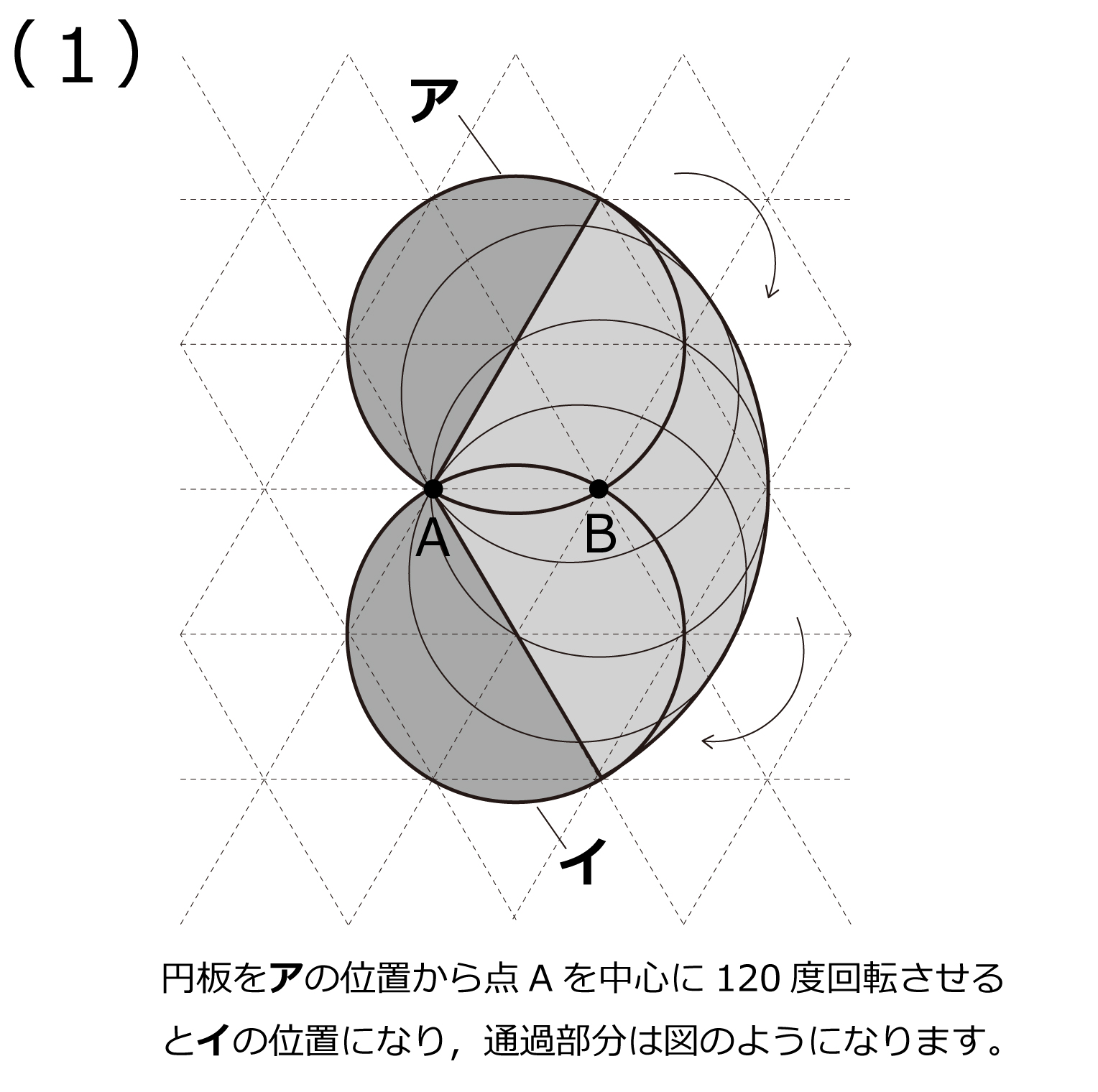
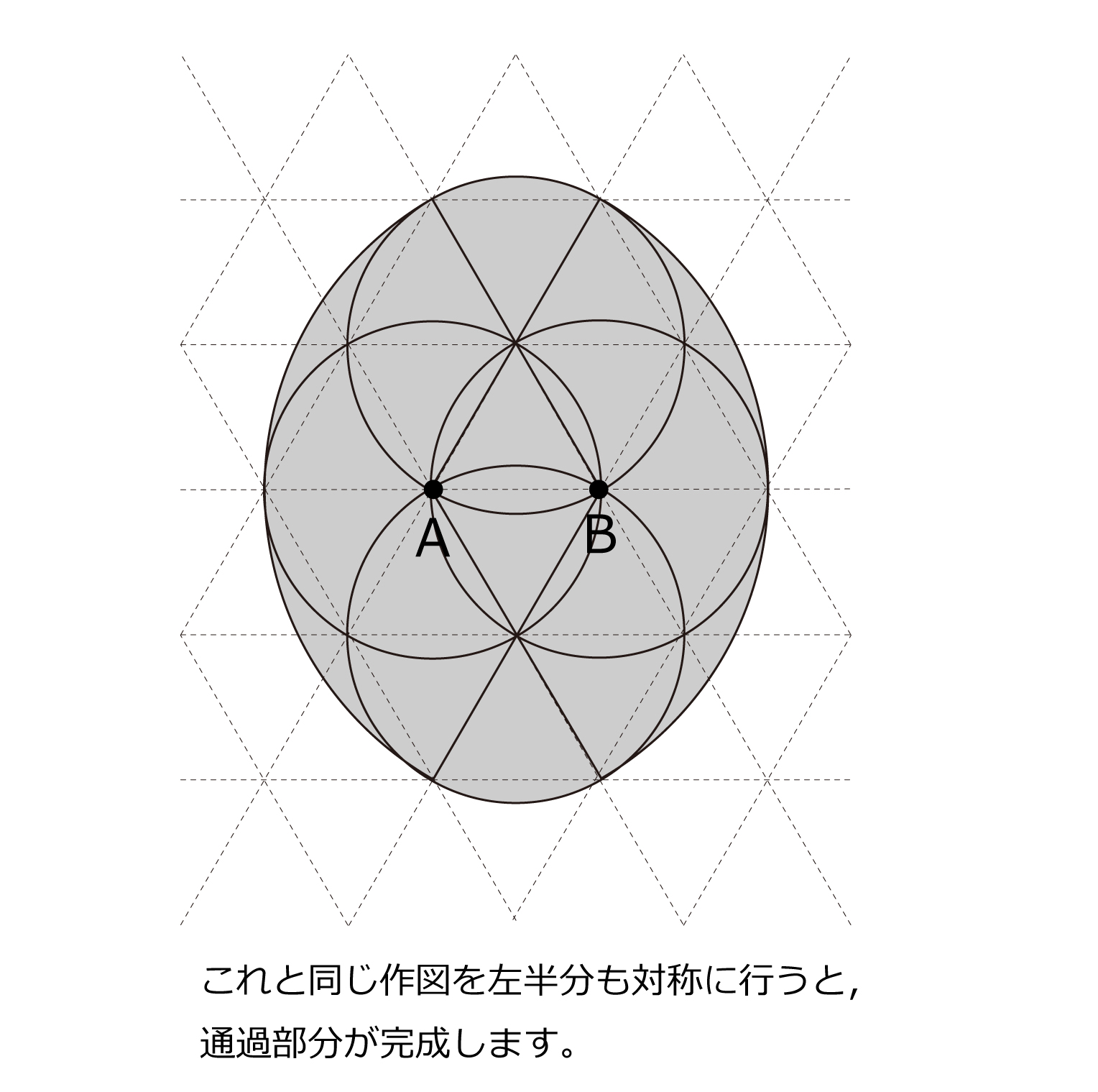
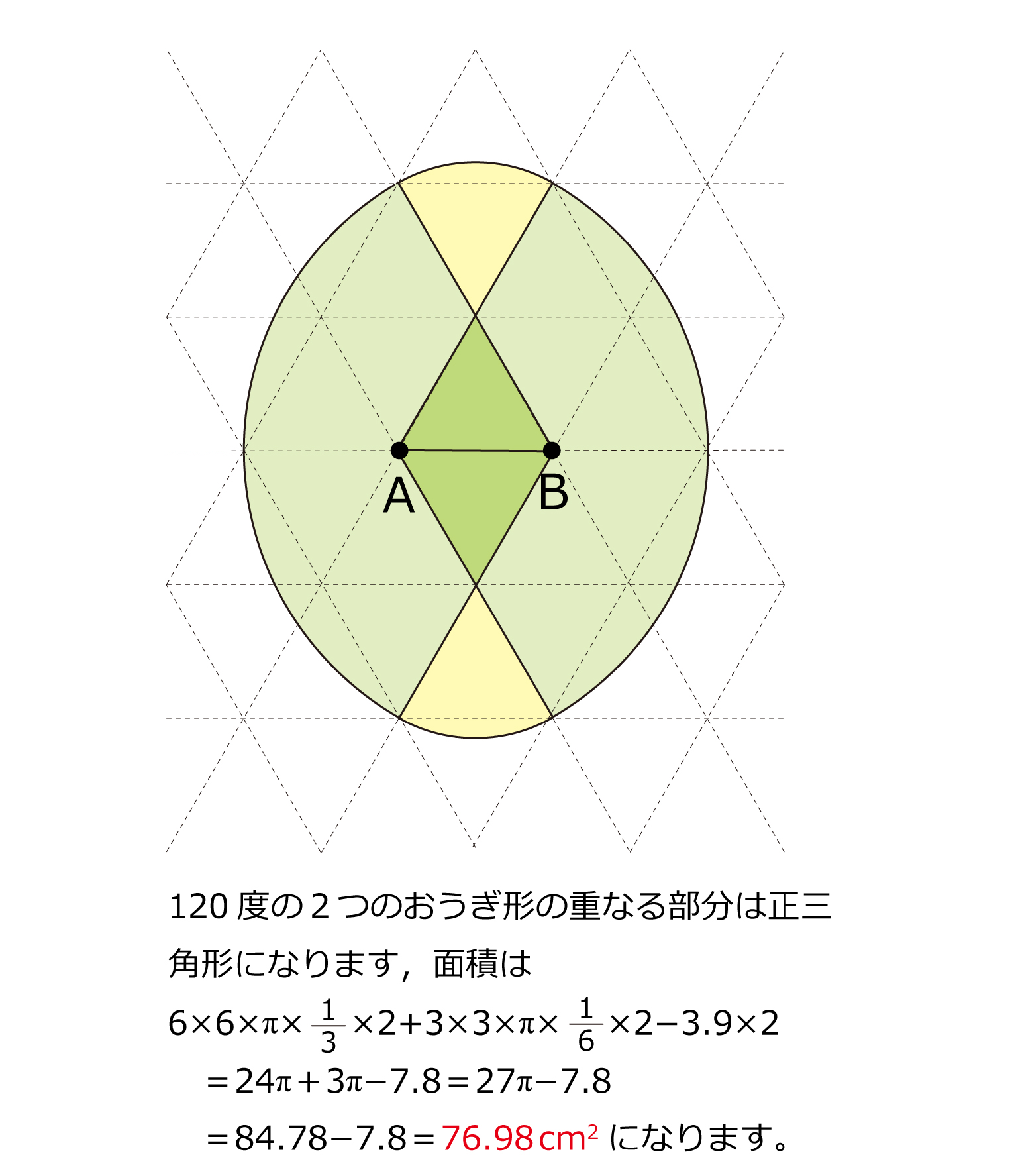

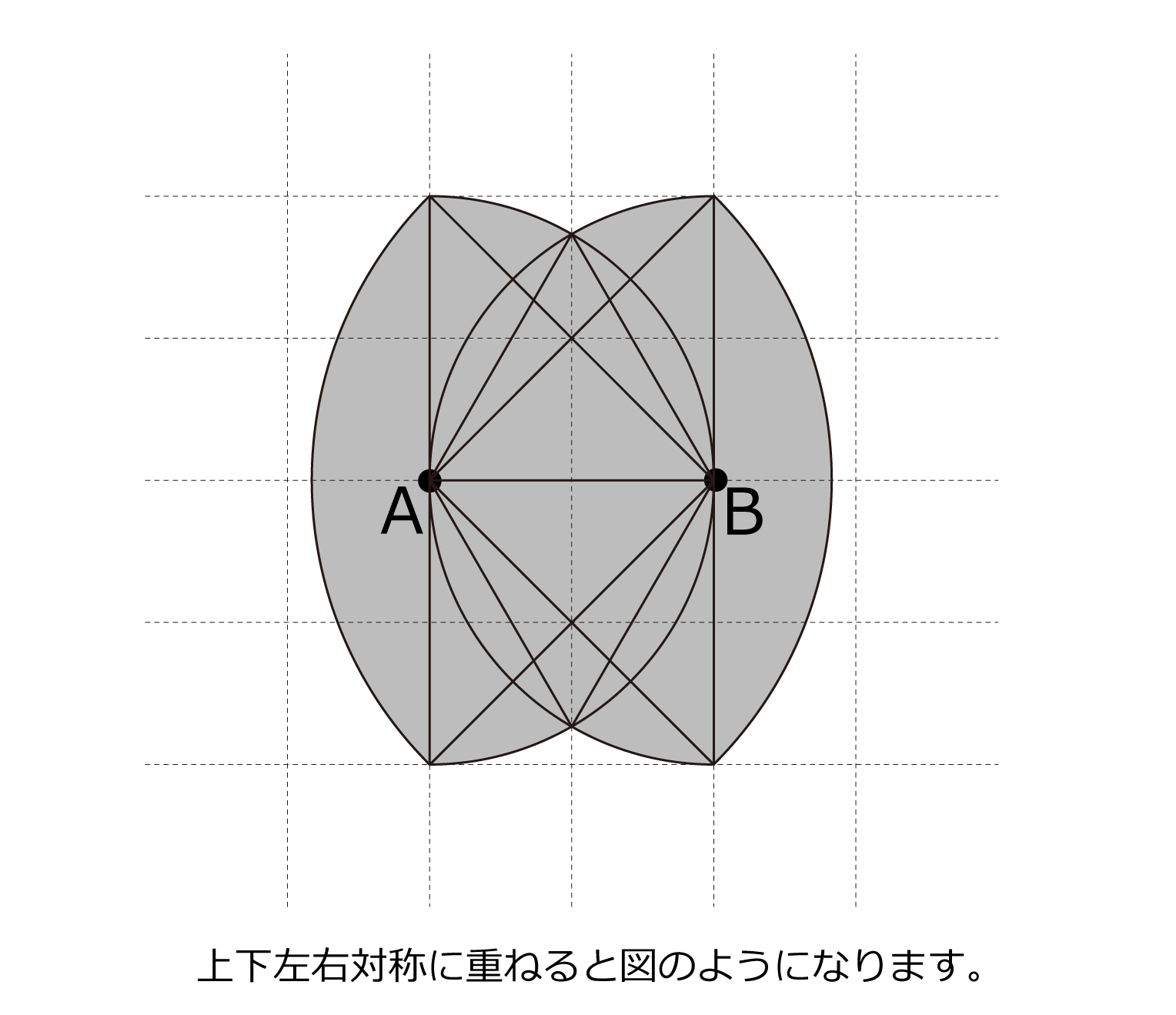
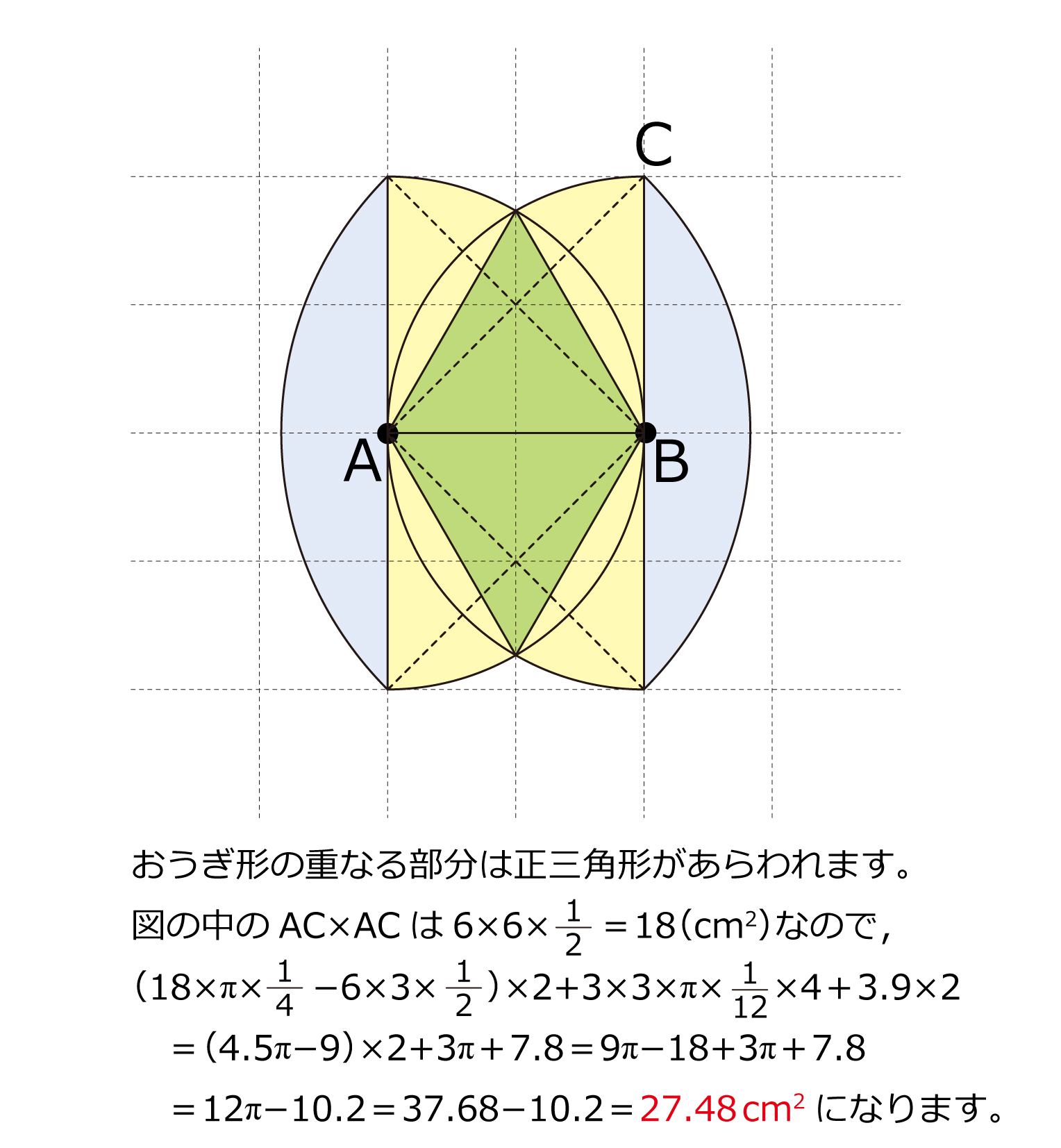
輪投げの通過部分はよくあるタイプですが,おうぎ形バージョンは珍しいなと思いました。