小学生の知の祭典 算数オリンピック!!
受験算数のトレンドを牽引するような新傾向問題の出題が多いことで有名でしょう。その中でも極めて高級な良問,面白い問題をできるだけ取り上げていきたいと思います。
実際の試験を改訂しているものもあるのでご了承下さい。
算数オリンピック
問題文
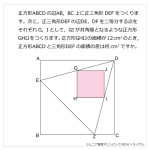
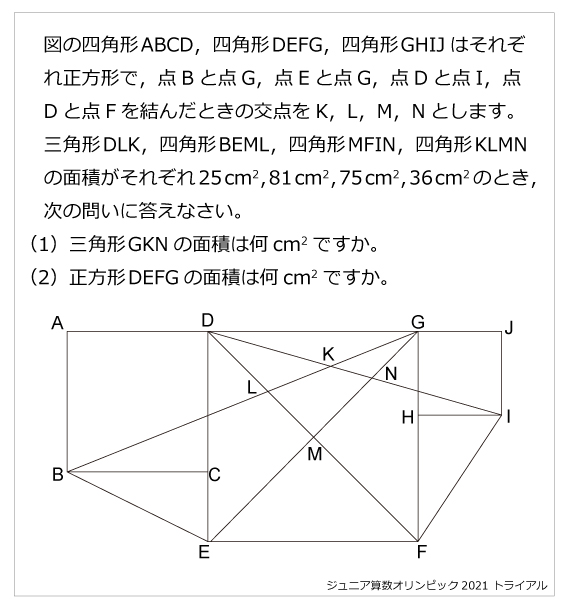
図の四角形ABCD,四角形DEFG,四角形GHIJはそれぞれ正方形で,点Bと点G,点Eと点G,点Dと点I,点Dと点Fを結んだときの交点をK,L,M,Nとします。三角形DLK,四角形BEML,四角形MFIN,四角形KLMNの面積がそれぞれ25cm2,81cm2,75cm2,36cm2のとき,次の問いに答えなさい。(1)三角形GKNの面積は何cm2ですか。
(2)正方形DEFGの面積は何cm2ですか。
解説
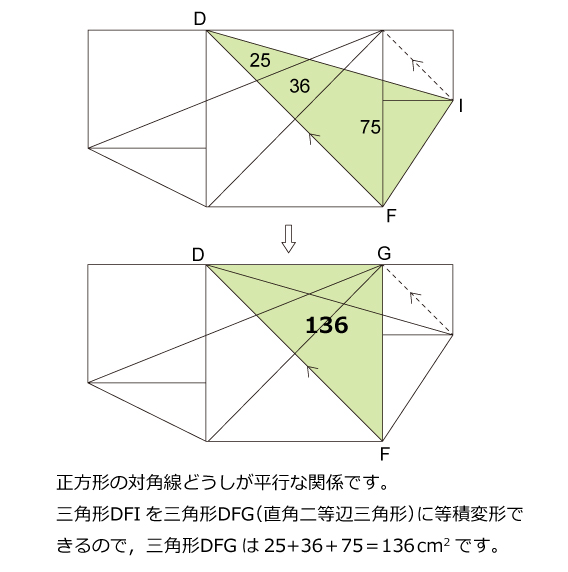
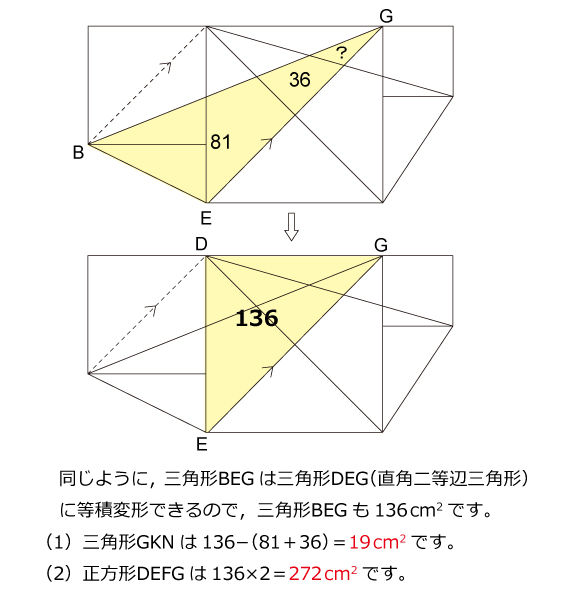
本質をわかっていなくてもなんとなくで正解してしまいそうですが,こういった補助線はしっかり押さえておきたいものです。

(2021年6月18日追記)
こちらの問題ですが,数値設定では図形が成立しなく全員に加点される対応となりました。(算数オリンピックHPより)
正方形DEFGの1/4である三角形DMG(272÷4=68)が,四角形DMGK(25+36+19=80)より上回っており図形不成立です。
こちらの問題ですが,数値設定では図形が成立しなく全員に加点される対応となりました。(算数オリンピックHPより)
正方形DEFGの1/4である三角形DMG(272÷4=68)が,四角形DMGK(25+36+19=80)より上回っており図形不成立です。