小学生の知の祭典 算数オリンピック!!
受験算数のトレンドを牽引するような新傾向問題の出題が多いことで有名でしょう。その中でも極めて高級な良問,面白い問題をできるだけ取り上げていきたいと思います。
実際の試験を改訂しているものもあるのでご了承下さい。
算数オリンピック
問題文
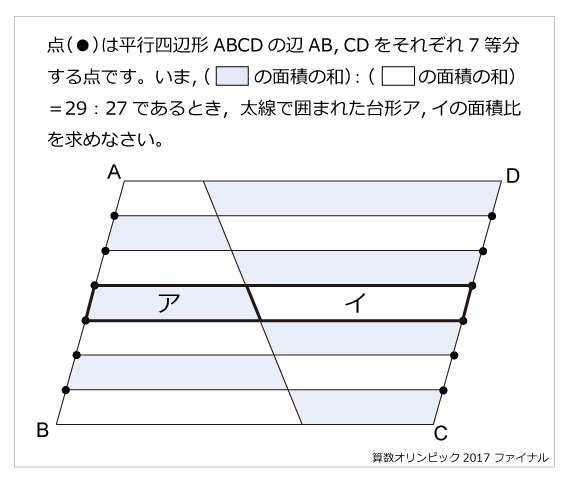
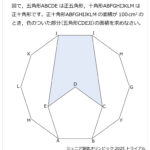
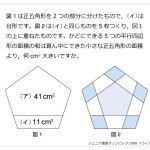
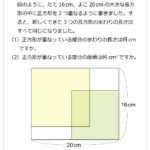
点(●)は平行四辺形ABCDの辺AB,CDをそれぞれ7等分する点です。いま,([色つき]の面積の和):([白色]の面積の和)=29:27であるとき,太線で囲まれた台形ア,イの面積比を求めなさい。解説
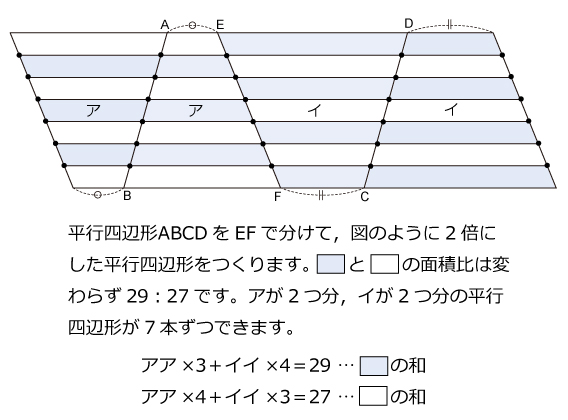

7月に行われた算数オリンピックファイナルの図形2問です。
思い入れのある(我が子のような)問題なので教室の壁に飾ることにしました。 pic.twitter.com/RhVHBZtoDy— 算数星人 (@sansu_seijin) 2017年7月30日
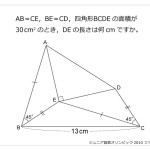
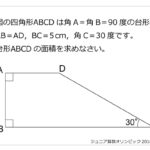
★もう一方の図形問題はこちら
→(算数オリンピック)2017年 jr.ファイナル












(29+27)÷7=8 … アとイの和
29ー27=2 … アとイの差
ここから和差算に持ち込んで解くこともできますね。正答率は高いでしょう。
2016年度は算数オリンピック作問大賞というものが催されておりました。
(BLOG記事)算数オリンピック作問大賞の結果が発表されています!! 算数星人もこっそり入賞していました(金賞でも銀賞でもなく…)
2017年度は別のかたちでこっそり関わっております(^_^;)