111top
少しプライベートな話から。
 
ちょうど近々，普段からお世話になっている算数の先生ら数名で集まっての食事会を予定しており，そこで持っていこうと思っていた問題のうちの1つをせっかくなのでこのBLOGでアップしてみたいと思います。(^_^;)
 
算数の先生ばかりが集まると話題も算数の話。この時期となると，入試問題の話ばかり。。。
 
解き方が割れる問題に関して，「どう解くのか？」「どう教えるのか？」がやはり話題になり，議論になります。
 
図形問題はいうまでなく，2017年度のその他ではやはり灘の2日目の速さが個人的には面白く，それを取り上げてみます。
 
誤解のないように言いますが，絶対にこの解き方が正しいとは思っていません。「こんな解き方があるんだあ〜」と少しでも多くの方の参考になればと思い投稿しました。
 
以下，実際に問題を解いていない方には少し退屈な内容になります。
 
 

2017年度 灘2日目［2］速さ

run

太郎君と次郎君はP地点を同時に出発し，855m離れたQ地点に向かいます。太郎君ははじめ分速240mで走ったのち，分速60mで歩き，そして分速120mでジョギングします。次郎君ははじめ分速120mでジョギングしたのち，分速240mで走り，そして分速60mで歩きます。二人はこのことを2日間繰り返しました。
（1）省略
（2）2日目，太郎君と次郎君の歩いた時間は同じで，太郎君と次郎君のジョギングした時間は同じで，さらに太郎君と次郎君の走った時間は同じでした。P地点を出発して3分後，走っている次郎君はS地点で太郎君を追い越しました。そして出発してから7分30秒後に同時にQ地点に着きました。P地点とS地点の間の距離は何mですか。

シンプルな設定だけどとても奥深い問題です。この問題が高級であることは云うまでもないでしょう。
 
私はこのように考えました。
 
全ての速さを分速60m減速し，歩かずに立ち止まったと仮定して考える
 
nadahayasa01
歩きの速さを0にして止めてみました。他の速さもその分減速して考えていきます。
 
ゴールまで7.5分間で着くので，この場合の進んだ距離は855−60×7.5＝405mになります。
 
これで複雑な条件が易しくなりました。
 
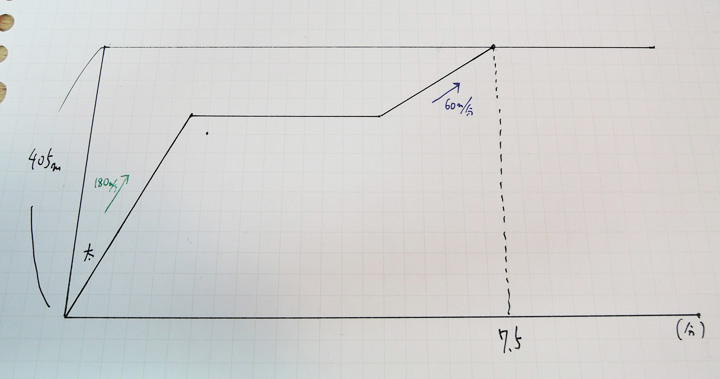
nadahayasa02
まず太郎君のダイヤグラムを描いてみました。
7.5分間で405m進みます。
 
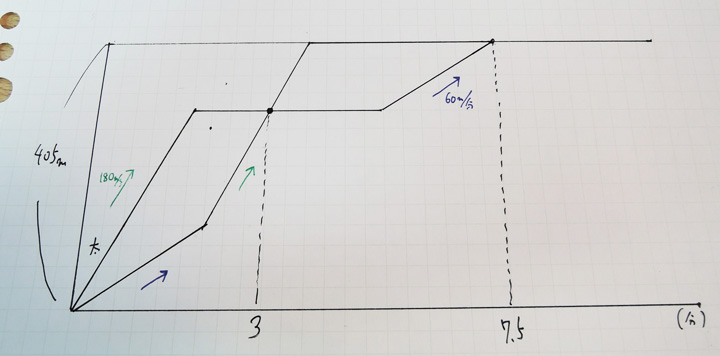
nadahayasa03
次郎君のダイヤグラムです。「次」という表記が抜けています。すいません。
 
ここで注意するのが太郎君の速さと平行でかつ同じ長さになるように線を引くことです。
 
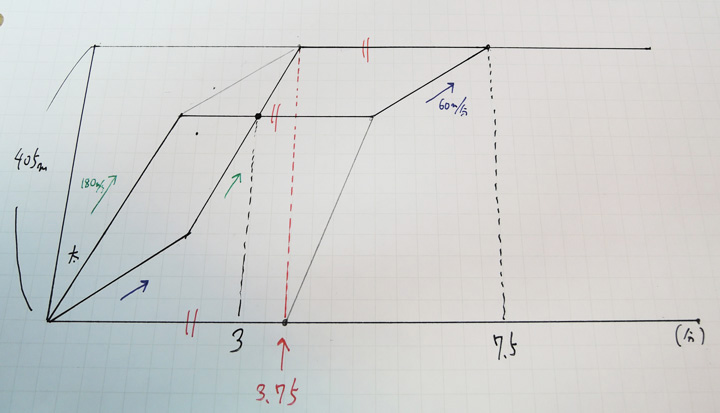
nadahayasa04
すると色々と平行四辺形ができることが分かります。
 
平行四辺形の等しい辺に注目すると，7.5分のちょうど半分の時間3.75分止まっていたことが分かります（このグラフの場合）。
 
次郎君に関して，このようなつるかめ算の計算で，走っていた時間とジョギングの時間が分かります。
 
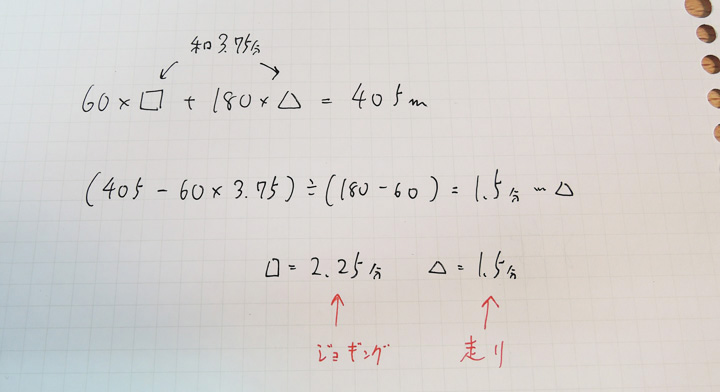
nadahayasa05
太郎君は初めに1.5分走り，ジョギングで3−1.5＝1.5分進んだところで次郎君に追い越されるので
 
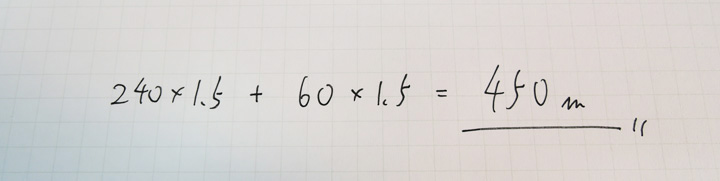
nadahayasa06
答えは450mになります。
 
色々と別解が発生しそうな問題ですが，考え方の参考になればと思います。
ここでは視覚的にも分かりやすいと思い，ダイヤグラム用いて解説しました。


こんな解法も返信いただきました。最後の計算がこちらの方がシンプルですね(^^)
 
 
色々やってみてスッキリしないときは立ち止まって（冷静になって），自分の知っているパターンに簡略化すると解けたりするものですね。
 
 
 
さて，新学年になり次の受験生の番ですね。合格目指して頑張りましょう！
 
gokkakei
大問1で出題された五角形の折り紙です。割り箸の袋を使って作りましたが，少し長さが足りませんでした。。。
食事の場で楽しめる算数ですね(^^)
 
 
 
↓1日目の解説はこちら
 
算数星人のWEB問題集：（2017年）灘中入試解説速報