算数が得意な小学生は高校生（大学生）になってから買って下さい。。。

まず，上記の書籍は小学生には全くオススメできないので，絶対に購入しないように！数学が得意な高校生や大学生向けの本だと思います。私はまだすべて読み終えていません。。。。
 
みなさんはラングレーの問題（wiki）をご存知でしょうか？
 

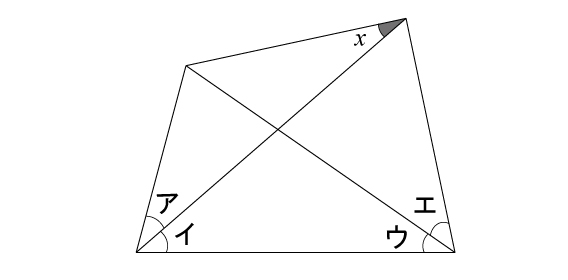
四角形の角ア，イ，ウ，エの値の条件で，角xの値を求めることができて，初等幾何の範囲内で証明できる問題

有名なものとして次のような問題があります（図は正確ではありません）。

 

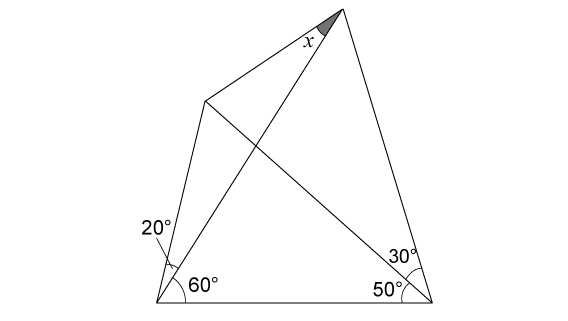
1922年にE.M.ラングレーが発表した問題で「ラングレーの最初の問題」と呼ばれているそうです。この問題にはエレガントな解答があるので，数学好きの方であれば一度はどこかで見たことあったり取り組んだことがあるのではないでしょうか？
 

中学受験レベルのラングレーの問題をやってみよう！

上の問題は算数がよっぽど得意な小学生でないと取り組めないかもしれません。入試問題レベル以上だと思います。
ですので今回は，中学受験生でも比較的取り組みやすいオリジナル問題を用意してみました。是非チャレンジしてみて下さい(^^♪
 

 
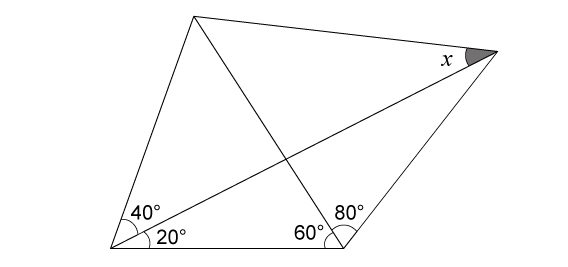
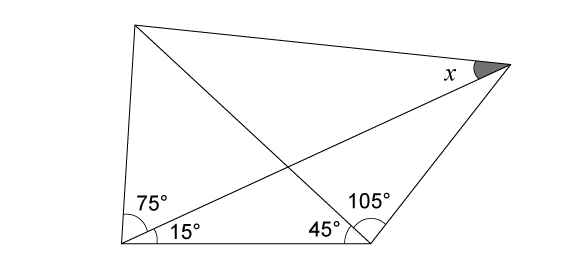
図は正確ではないので，画用紙でしっかり作図して考えましょう！
 
 
ウォーミングアップはここまでです。ではラングレーの最初の問題に挑戦してみましょう！
 

 

さあ！ラングレーの問題にトドメをさしましょう！
この問題の解答はスクロールしていくと出てきます。
 
 
 

（解き方1）正三角形をつくる王道の解法

 

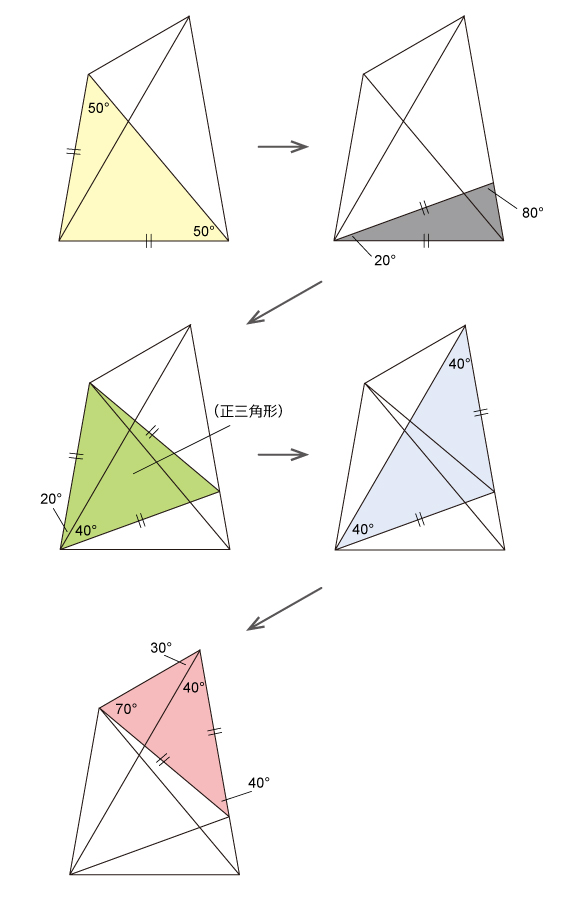
思わぬところに正三角形を作図すると，エレガントに答えを導けました。この解き方が王道でしょう。40度・70度・70度の二等辺三角形ができるので角x＝30度です。
 
 

（解き方2）対称性に注目する方法

 

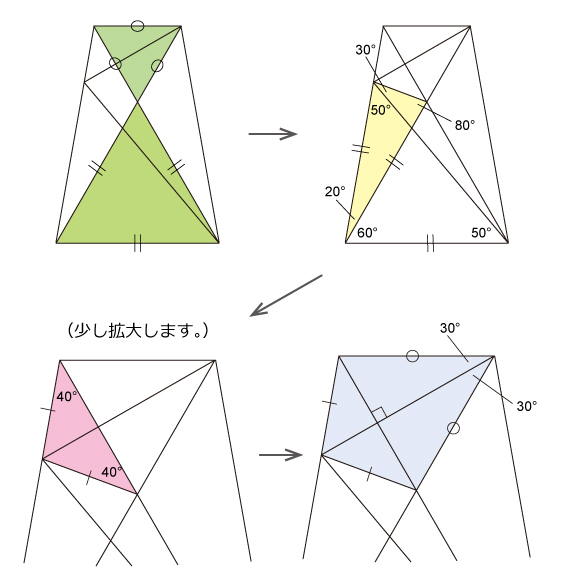
青色の部分が2つに二等辺三角形を合わせた四角形なので対角線が垂直に交わります。そして，角xが60÷2＝30度だとわかります。
 
解法・証明は他にも色々あるそうですが，小学生でも理解できるのはこの2つぐらいだと思います。
 
 

なんと！ラングレー問題にはとてもエレガントな図形が隠れていました！

 

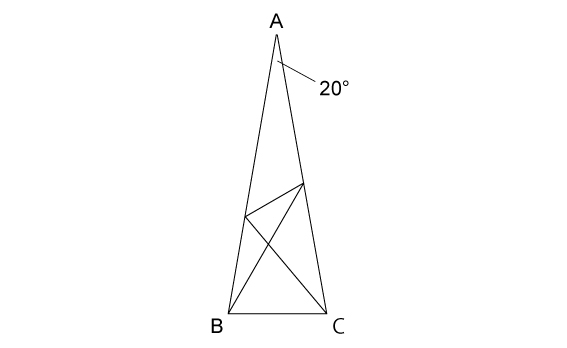
四角形の2辺を上の図のように延長させると，AB＝ACの二等辺三角形ABCができます。この二等辺三角形を利用しても解法が見つかりそうです。
 
頂角が20度の二等辺三角形ABCを18個並べると正十八角形ができます。
 

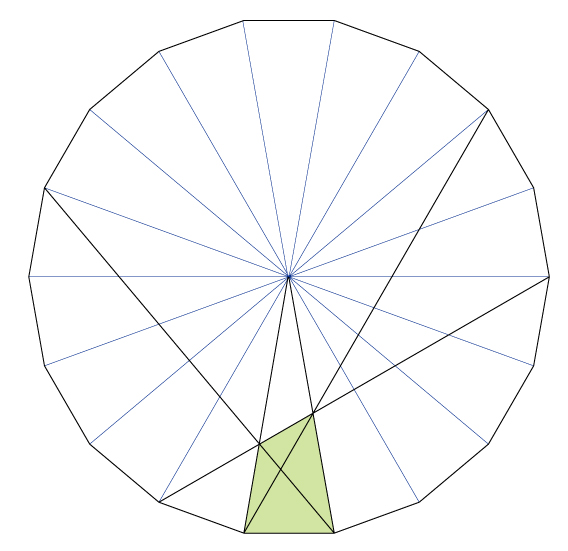
なんと驚くことに！この正十八角形の対角線を結ぶと，問題になっている四角形を作ることができるのです！
いや～！ラングレーの問題ってすごく奥が深いですね(^^♪
 
 
（この記事はamebaなどの過去記事を再編集したものです）