すごく今更ですが，
本屋大賞を取り，映画化もされた時代小説『天地明察』を取り上げたいと思います。

科学好きと歴史好きの両者が楽しめる小説です！

江戸時代，改暦（日本独自の暦の作成）に捧げた渋川春海の一生を描いた作品なのですが，
 
物語の中で，春海が算額の問題を考えたり，自ら作問したりと，いくつか算術問題が登場することも，理系読者を惹きつけるこの小説の人気の1つなのではないでしょうか。
 
もちろん，江戸のお城事情も描写されており，時代劇好きにも楽しめます。渋川春海は囲碁にも通じており，それらも物語に登場します。とにかく渋川春海は多才なのです(^^)
 
今回はその中でも，
物語序盤，渋川春海が全然分からなくて，関孝和が一瞥即解した問題をご紹介します。
 
一瞥即解（いちべつそっかい）
意味：ちらっと見ただけですぐ分かるという意味
 
小説を読まれて，算法の解法が分からなかった方は，是非ご参考にして下さい。
 

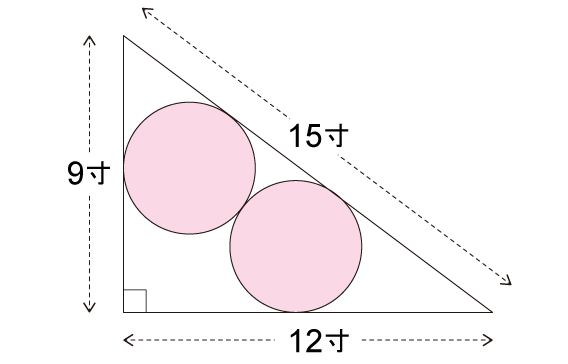
今，釣（高さ）が9寸，股（底辺）が12寸の勾股弦（直角三角形）が有る。その内部に，図の如く，直径が等しい円を二つ入れる。円の直径を問う。

（小説では15寸の長さは与えられていません。）

直角三角形の内部に2つの同じ円が内接していて，その円の直径を求めよ。

という問題です。
 

3：4：5の直角三角形の予備知識を確認

さて，解説にいく前に，まずはこの問題（題材）の予備知識を少し。
 

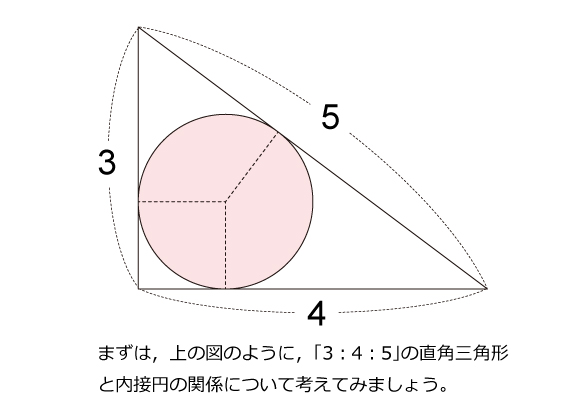
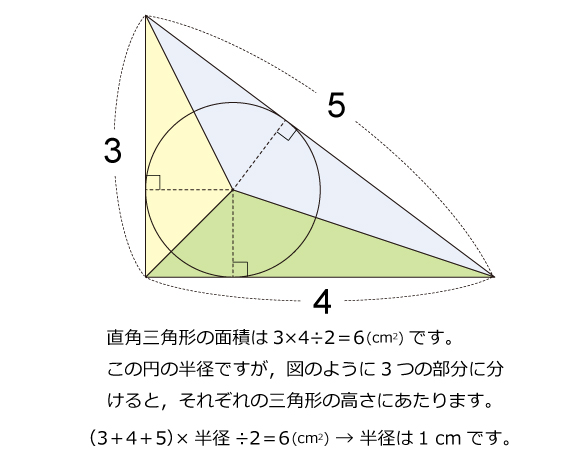
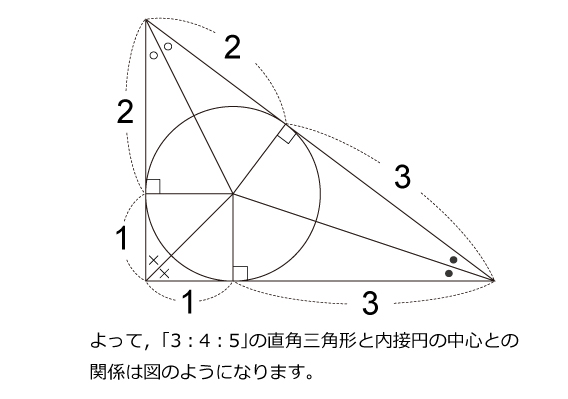
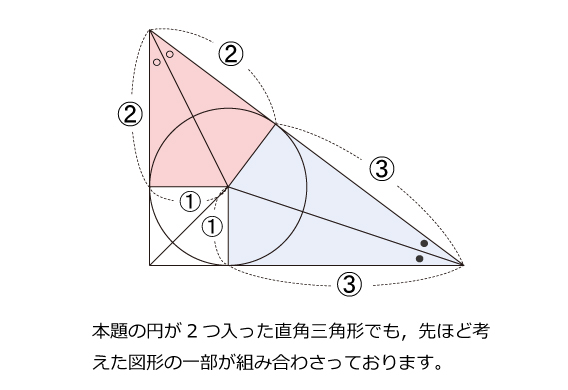
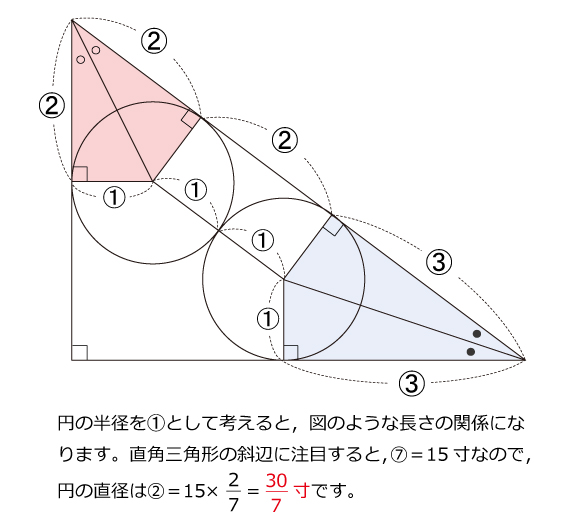
3：4：5の直角三角形を題材にした問題は，よく中学受験の入試問題でも出題されるので，押さえておきましょう。
 

アクロバティックな別解

このような別解も存在しています。補助線を引き，合同な三角形を作図して考えます。
 

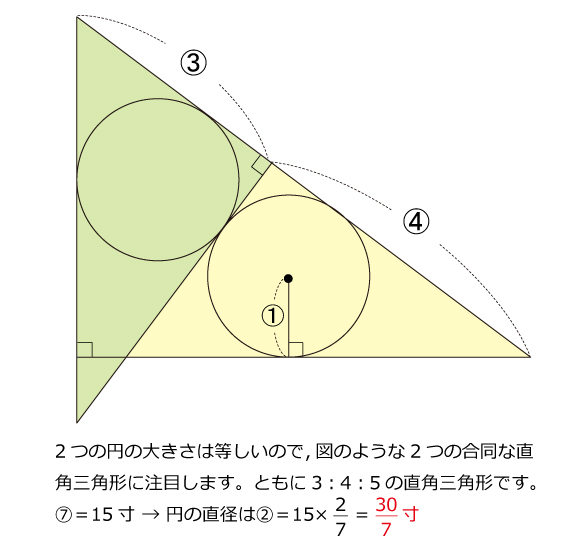
皆さんはみごと「明察！」することができたでしょうか？
 
さて，江戸の和算家 関孝和はどのような解法で一瞥即解したのかがすごく気になります^_^;。
それを想像するのも読書の楽しみの1つです。
 
 
（この記事はamebaなどの過去記事を再編集したものです）