印象に残った入試問題の良問を「今年の1問」と題して取り上げています。志望校への腕試しや,重要項目の確認に是非ご活用下さい。
実際の試験を改訂しているものもあるのでご了承下さい。
駒場東邦中
問題文
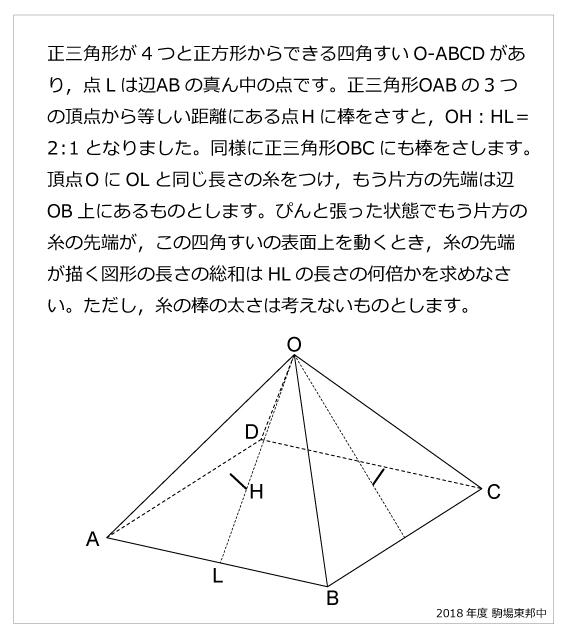
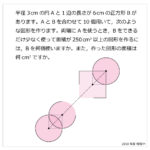
正三角形が4つと正方形からできる四角すいO-ABCDがあり,点Lは辺ABの真ん中の点です。正三角形OABの3つの頂点から等しい距離にある点Hに棒をさすと,OH:HL=2:1となりました。同様に正三角形OBCにも棒をさします。頂点OにOLと同じ長さの糸をつけ,もう片方の先端は辺OB上にあるものとします。ぴんと張った状態でもう片方の糸の先端が,この四角すいの表面上を動くとき,糸の先端が描く図形の長さの総和はHLの長さの何倍かを求めなさい。ただし,糸の棒の太さは考えないものとします。解説
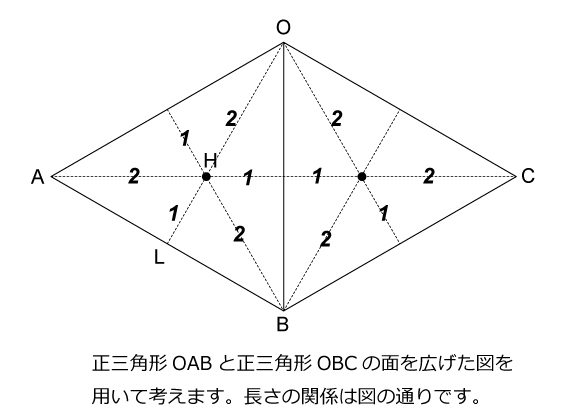
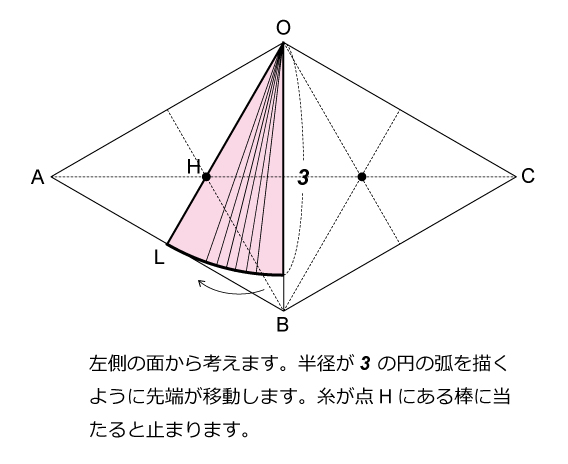
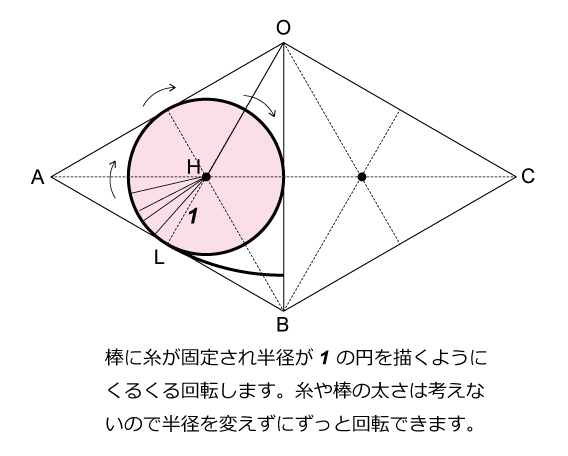
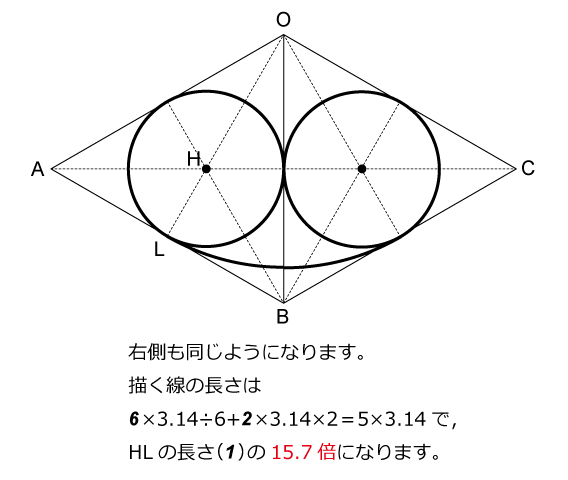
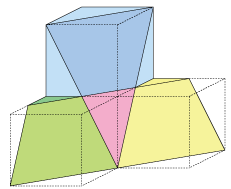
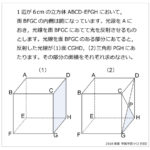
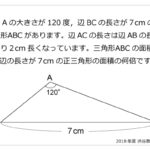
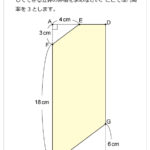

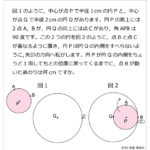










この問題は非常に問題文の条件が複雑で,どういった操作をするのか混乱した受験生が多かったのではないかと予測できます。この問題の前問などは確実に正解しておきたい難易度でした。