印象に残った入試問題の良問を「今年の1問」と題して取り上げています。志望校への腕試しや,重要項目の確認に是非ご活用下さい。
実際の試験を改訂しているものもあるのでご了承下さい。
慶應義塾中等部

問題文
ある整数を,3つの平方数の和で表すことを考えます。例えば,4や14は,4=0^2+0^2+2^2,14=1^2+2^2+3^2のように,3つの平方数の和で表すことができます。1から100までの整数のうち,3つの平方数の和で表すことのできない整数は全部でいくつありますか。解説

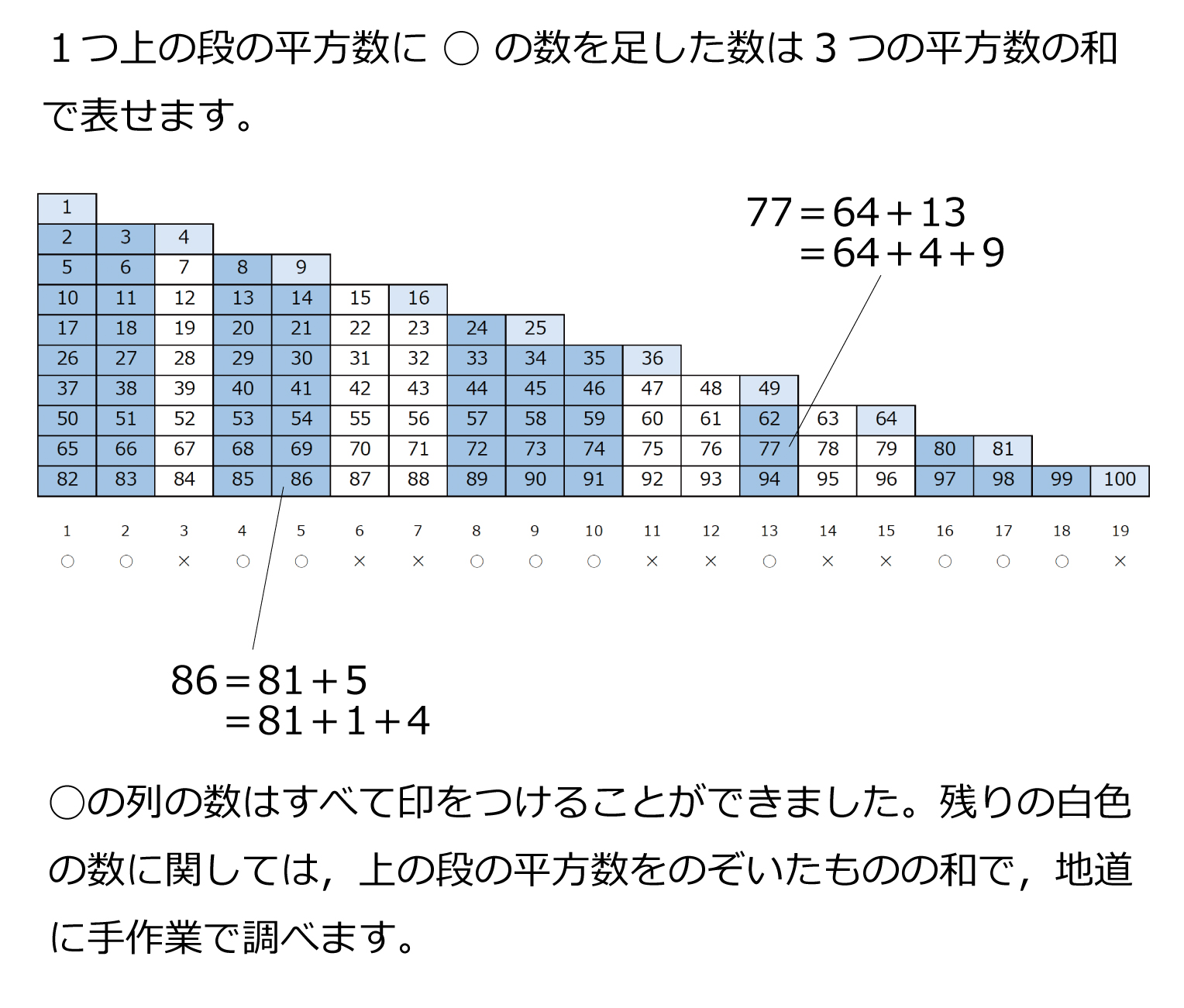
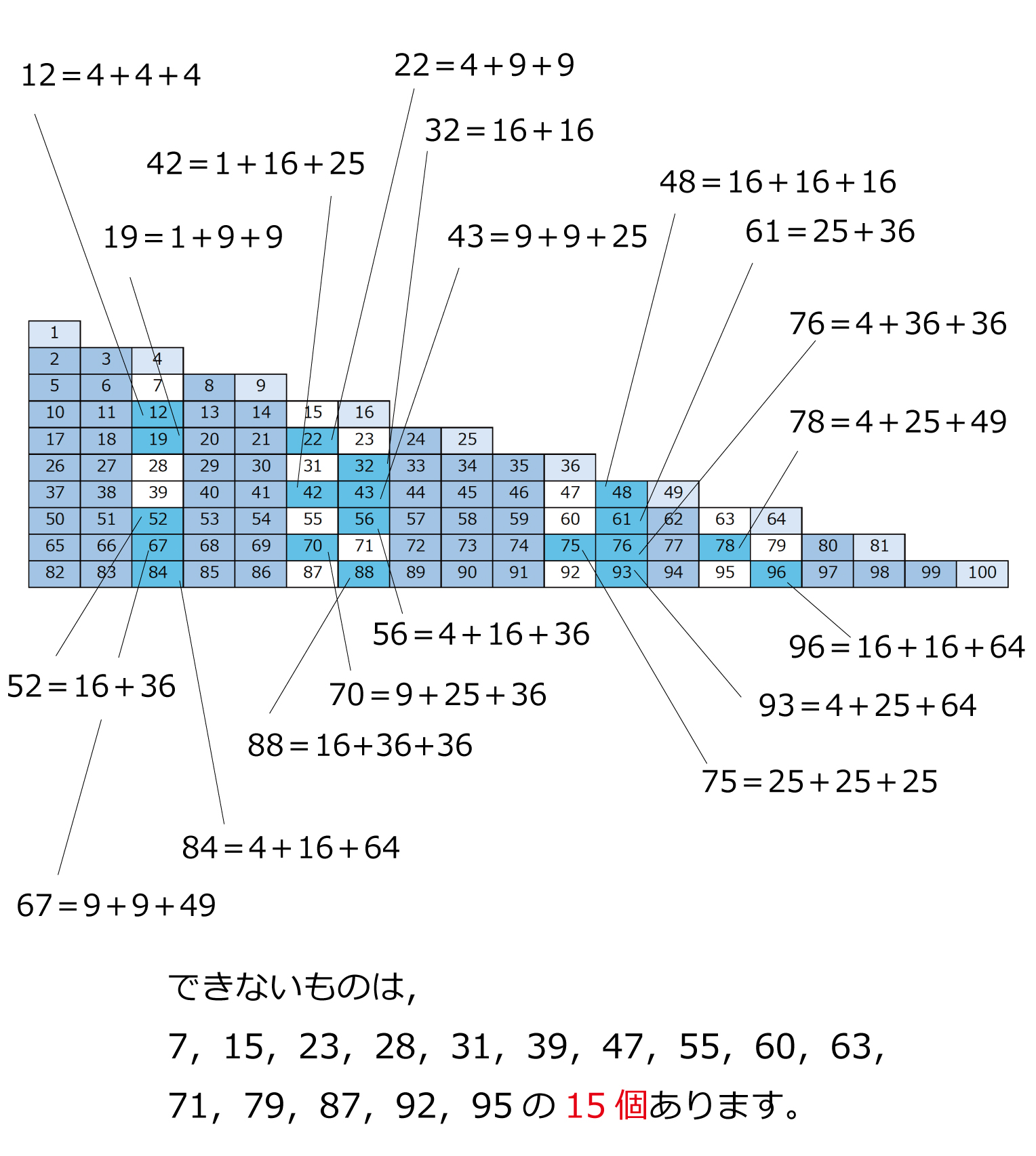

















調べると,
ガウス・ルジャンドルの定理(三平方和定理)→wiki
と呼ばれるもので,
3つの平方数の和で表せないものは4^n(8k+7)となるようです。
8で割ると7余る数が7,15,23,31,39,47,…で
それの4倍の数 28,60,92,…や16倍,64倍の数があてはまるようです。
もちろん証明や説明は中学受験範囲では不要です。