印象に残った入試問題の良問を「今年の1問」と題して取り上げています。志望校への腕試しや,重要項目の確認に是非ご活用下さい。
実際の試験を改訂しているものもあるのでご了承下さい。
桜蔭中
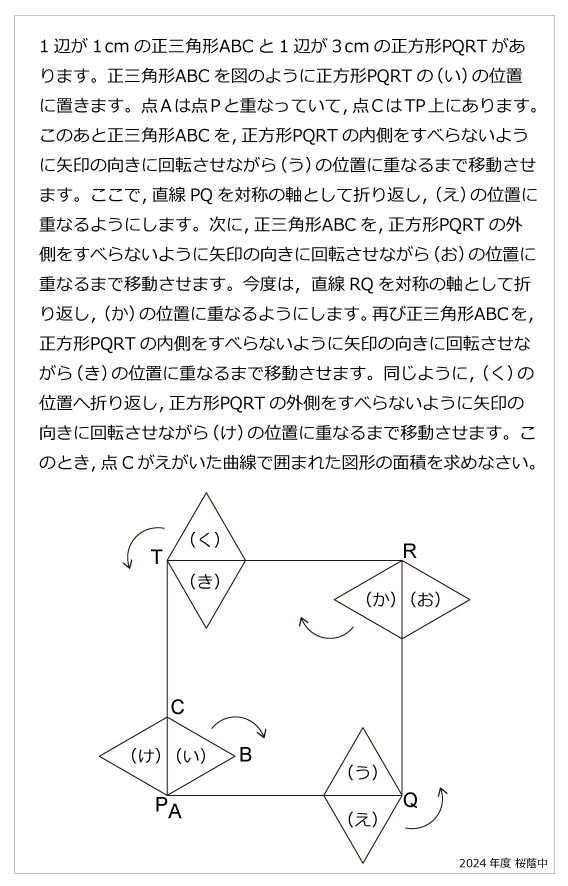
問題文
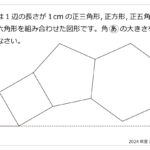
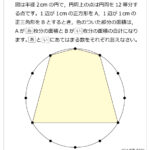
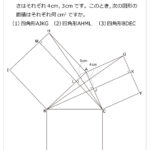
1辺が1cmの正三角形ABCと1辺が3cmの正方形PQRTがあります。正三角形ABCを図のように正方形PQRTの(い)の位置に置きます。点Aは点Pと重なっていて,点CはTP上にあります。このあと正三角形ABCを,正方形PQRTの内側をすべらないように矢印の向きに回転させながら(う)の位置に重なるまで移動させます。ここで,直線PQを対称の軸として折り返し,(え)の位置に重なるようにします。次に,正三角形ABCを,正方形PQRTの外側をすべらないように矢印の向きに回転させながら(お)の位置に重なるまで移動させます。今度は,直線RQを対称の軸として折り返し,(か)の位置に重なるようにします。再び正三角形ABCを,正方形PQRTの内側をすべらないように矢印の向きに回転させながら(き)の位置に重なるまで移動させます。同じように,(く)の位置へ折り返し,正方形PQRTの外側をすべらないように矢印の向きに回転させながら(け)の位置に重なるまで移動させます。このとき,点Cがえがいた曲線で囲まれた図形の面積を求めなさい。解説
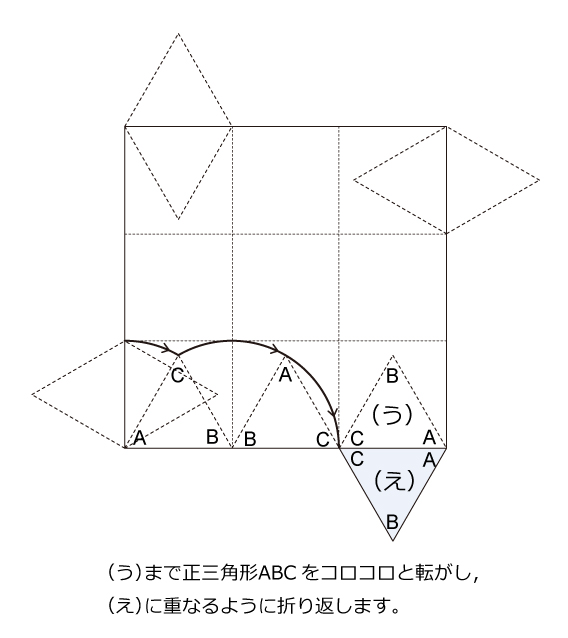
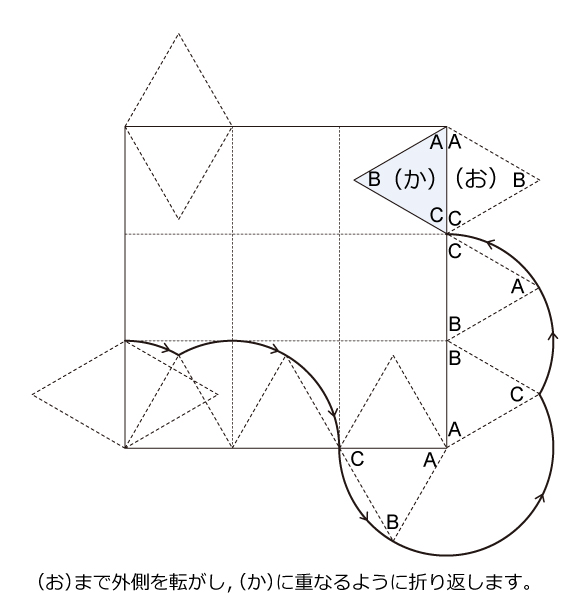
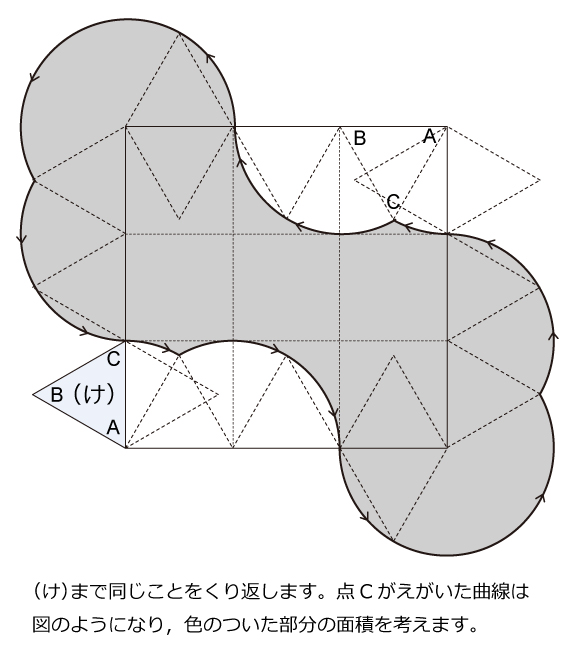
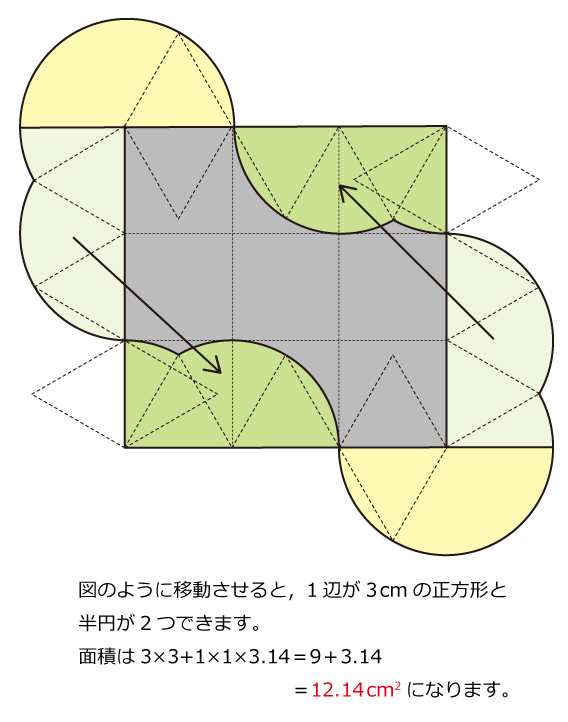
複雑な回転移動ですが,半分の段階まで完成すると残りはラクでしょう。