本日から新企画をスタートしたいと思います。
題して「小学生でもわかる塵劫記」です!!

塵劫記(じんこうき)とは,江戸時代の算術の教科書です。和算,算法に関してはこのBLOGでも度々取り上げている話題です。
過去BLOG記事-13才の少女がくり広げる江戸の数学小説「算法少女」約40年前に出版された傑作!
過去BLOG記事-「ススメ!算法少年少女」和算に関する決定版といえるでしょう!
江戸時代は大きな戦さも少なく,江戸(東京)などは都市として非常に発達しており,当時の世界一の人口を誇っていたことは有名な話です。庶民の識字率なども非常に高かったようで,武家などの特権階級でない庶民もこの塵劫記を読んで勉強をしていたようです。
不思議なことで,江戸時代のこの算術書がベストセラーかつロングセラーとなったほど,我々の祖先は勉強好き(数学算数好き)だったのです。
江戸時代の人々が,神社に算額奉納して算法を楽しんだのは過去にBLOGで紹介したとおりです。
-過去BLOG記事-(大阪上本町すぐ)宅間流の算額を拝みに生國魂神社へ行ってきた
-過去BLOG記事-インベスターZをご存知ですか?今週は塵劫記の油分け算も登場!
この連載企画では,江戸のベストセラー「塵劫記」を題材に,小学生でもわかる問題・解法を取り上げていきたいと思います。
可能な限り継続できるよう更新をがんばっていきます^^;
記念すべき第1回は「俵杉算」です。
俵杉算(三角数や連続する自然数の和)
俵杉算(たわらすぎざん)

ここでいいう俵とは米俵のことでしょう。
俵をピラミッド状に積むことを杉形(すぎなり)と言ったり,杉に積むと言います。
積まれた俵を瞬時に数を数える計算方法を俵杉算と呼びます。
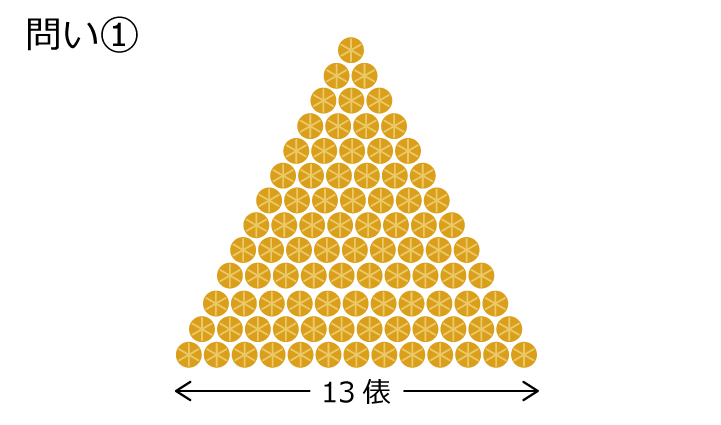
「米俵はぜんぶで何俵ありますか?」
-塵劫記での解き方-
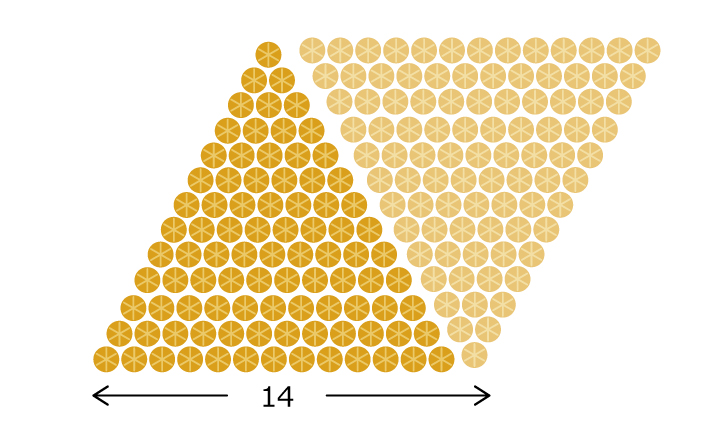
同じものを2セット用意して逆向きにして並べます。
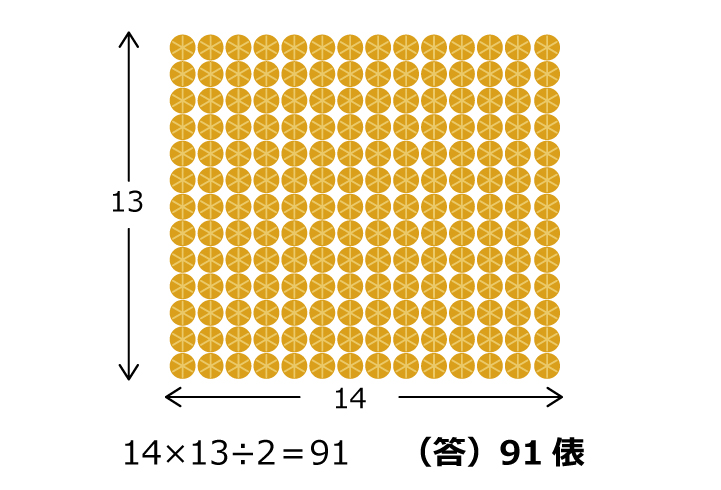
1+2+3+4+…+9+10の計算を,
(1+10)×10÷2=55の計算で求める方法と同じです。
1+2+3=6や
1+2+3+4=10は,三角形のかたちに並べるので,三角数と呼ばれていますね。

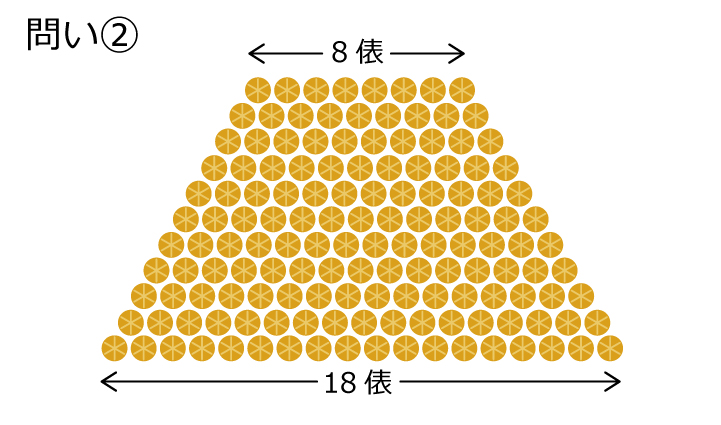
「米俵はぜんぶで何俵ありますか?」
-塵劫記での解き方-
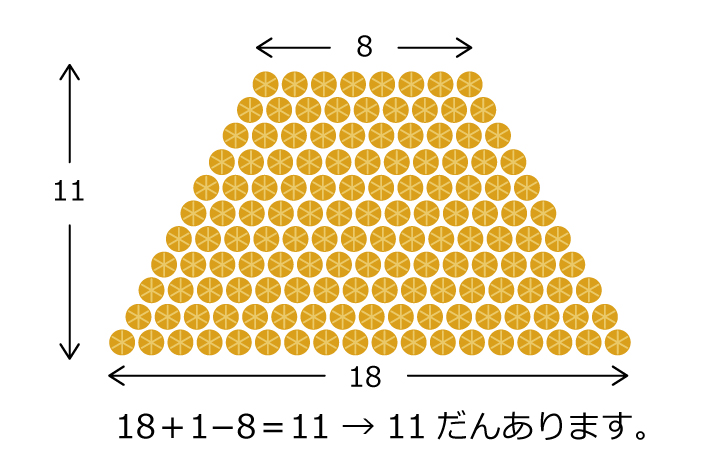
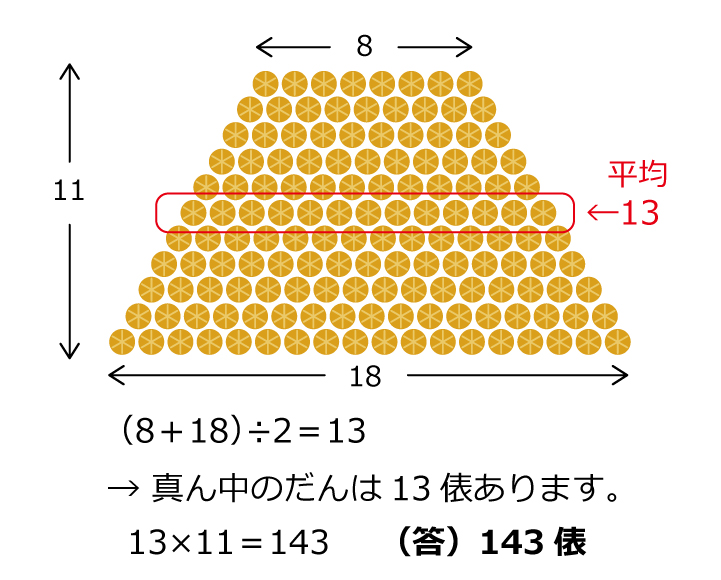
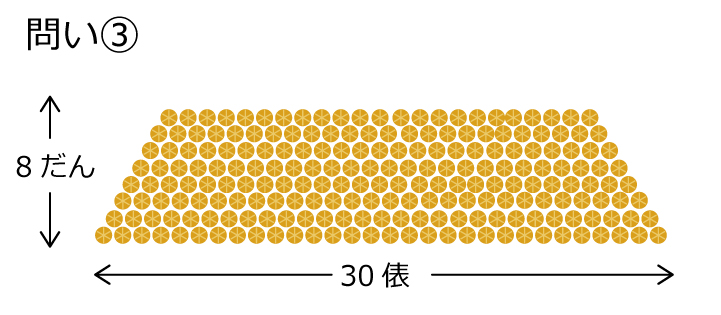
「米俵はぜんぶで何俵ありますか?」
-塵劫記での解き方-
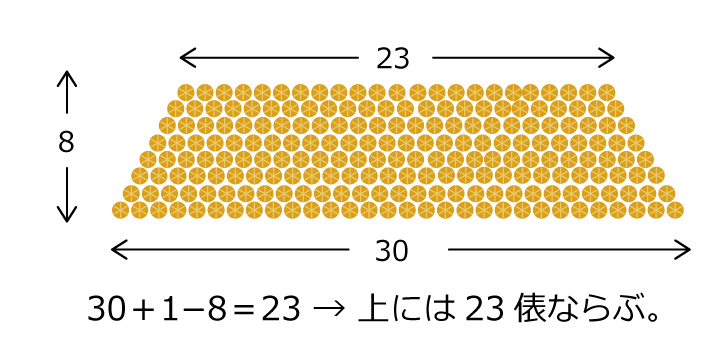
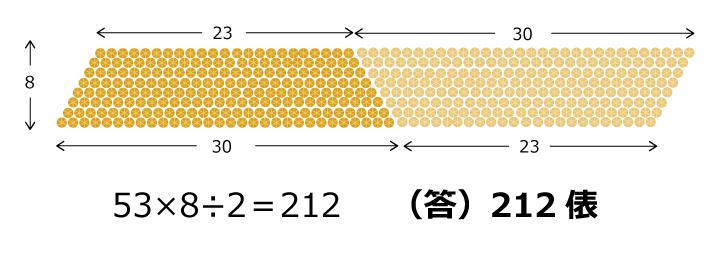
商人が,蔵に入れられた大量の俵を数えるとき,この計算方法を知っていないと致命的な気がします。。。
以上になります。いかがでしょうか。
第1回はすごく易しめでしたね。徐々に難しいものも扱っていきます。
<P66-68 一目録 第十二「俵すぎざんの事」を参照>

寛永11年版の電子画像はこちら


(ソース)阪本龍門文庫善本電子画像集
つづき【和算】第2回「入れ子算」小学生でもわかる塵劫記-じんこうき-